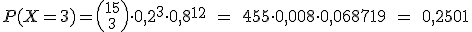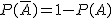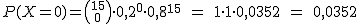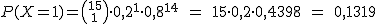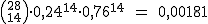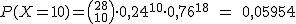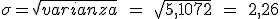3.2. Y aplicamos el modelo
 |
| Imagen de tatrebil bajo licencia Creative Commons |
Ahora ya sí, tenemos todo lo necesario. Sabemos lo que es la distribución binomial y sabemos calcular los números combinatorios, así que, ya podemos calcular probabilidades de una distribución binomial. Bueno, en realidad podíamos hacerlo pero lo que ocurre es que sería pesadísimo. Por ejemplo, si Gonzalo juega 10 veces y queremos calcular la probabilidad de que pierda 4 veces, tendríamos que hacer un árbol con 10 ramificaciones y contar en las que pierde 4. No te digo más que ese árbol completo tendría 1024 ramitas. Uff! ¡Casi nada!
Vamos a aprovechar que es una binomial y que en este modelo las probabilidades se calculan así:
Si X es una variable aleatoria binomial de parámetros n y p, X~B(n , p), la función de probabilidad de esta variable X viene dada por:
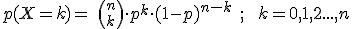
Es decir, si X~B(n,p) la probabilidad de que X tome el valor K, con k comprendido entre 0 y n, se calcula a partir de esa fórmula.
En una distribución binomial B(n , p), calcular la esperanza o media y la varianza es muy fácil, pues basta aplicar estas dos fórmulas:
Media: μ = n·p
Varianza: σ2 = n·p·(1-p)
Así, por ejemplo, en el caso del examen de tipo test habíamos visto que fallarlas todas tenía una probabilidad muy baja, que lo lógico era que se acertara alguna, pero, ¿cuántas se puede esperar que acierte? Pues el valor esperado es la media, de ahí que se llame también esperanza, y si la calculamos obtenemos:
μ = n·p = 10·0,25 = 2, 5
Luego el valor esperado de preguntas acertadas es 2,5.
 |
| Imagen de ArminFlickr bajo licencia Creative Commons |
A la salida de uno de los casinos a los que van de vez en cuando Blanca y Gonzalo hay unos cuantos bares y restaurantes a los que les gusta ir. La mitad de las veces van a Casa Giráldez, el 10% de las veces al Mesón Serrino, y el resto de las veces, o van al restaurante Loreda o al Bar La Tertulia.
En este último local trabaja un amigo nuestro Manolo y siempre que los ve entrar en el casino se pregunta si irán después a su bar, pues las propinas que dejan, especialmente cuando ganan, son de las que no se olvidan. En el último trimestre, Blanca y Gonzalo han ido 15 veces al casino. ¿Cuántas veces puede esperar Manolo que vayan a su bar? ¿Con qué probabilidad se dará ese suceso?Y si no van tantas veces, ¿cuál la probabilidad de que al menos vayan dos veces?
 |
| Imagen modificada de Contando Estrelas bajo licencia Creative Commons |
Siguiente ejemplo. ¿Te acuerdas de nuestra compañía de reparto y mensajería TRANS VELOX de las primeras unidades? Pues también ellos en sus previsiones de reparto utilizan la distribución binomial.
No sé tú, pero a mí más de una vez me han traído un paquete a casa y justo en el momento que han venido no había nadie. ¡Son cosas que pasan! Cuando esto ocurre, te llaman por teléfono para que des otra dirección o un lugar donde dejar el paquete, pero también puede ocurrir que no logren ponerse en contacto contigo y entonces el paquete vuelva a la central.
En la sede de Mérida llevan muchos años ya funcionando y entre otros lugares, a uno de los que más paquetes llevan es a Almendralejo. En esta ciudad los trabajadores de TRANS VELOX tienen estimado que en el 60% de los casos, en el domicilio donde se ha de entregar el paquete no hay nadie, y de estos en el 40% de los casos el repartidor no consigue contactar telefónicamente con el cliente, con lo que el paquete va devuelto a Mérida hasta otro día de reparto.
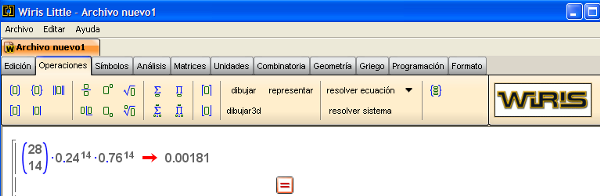
Pues bien, un lunes tienen 28 paquetes que repartir en Almendralejo. ¿Con qué probabilidad no se entregan la mitad de los paquetes? ¿Con qué probabilidad se devuelven 10 paquetes? ¿Qué número de paquetes se espera que entreguen correctamente? ¿Hay mucha desviación en esa previsión?
En la siguiente escena de GeoGebra puedes ver gráficamente como se comporta la distribución binomial y calcular cualquier probabilidad, siempre que "n" sea 50 como máximo.
Puedes comprobar que se cumple lo que dijimos en el caso del bar, que el valor que tiene la probabilidad mayor es la media de la variable, o los valores cercanos si ésta no es un número entero.
Applet Geogebra de Manuel Sada bajo licencia Creative Commons.
|
a) Ninguna porque es muy raro ese grupo
| |
|
b)1.320.000
| |
|
c) 1.320
|
|
a) 0,60
| |
|
b) 0
| |
|
c) 0,3
|
|
a) 0,0051
| |
|
b) 0,051
| |
|
c) 0,51
|

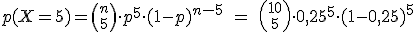
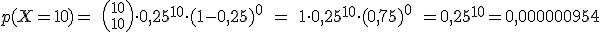
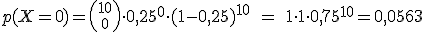
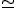 0,0781; un 7,81%
0,0781; un 7,81%