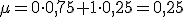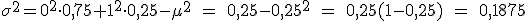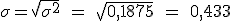2. Blanco o negro
 |
| Imagen de tnarik bajo licencia Creative Commons |
En numerosas situaciones, una pregunta sólo tiene dos posibles respuestas, sí o no, y en numerosos experimentos, sólo son posibles dos resultados, blanco o negro, me gusta un modelo de coche o no me gusta, una persona toma café o no toma, un ladrillo es defectuoso o está en buen estado, una persona está enferma o sana,..., y así, hasta que nos aburramos, podemos estar poniendo ejemplos de situaciones en las que sólo hay dos posibilidades.
Bueno, pues esto que puede parecerte tan tonto, resulta que en el mundo de las probabilidades es la base con la que se resuelven muchas cuestiones, hasta el punto incluso de decidir si una partida de zumos es defectuosa y no es apta para el consumo. Pero vamos por parte, un experimento aleatorio en el que sólo hay dos posibles resultados se denomina Experimento de Bernoulli, y a esos dos posibles resultados que constituyen el espacio muestral se les llama éxito y fracaso.
¿Y se puede definir una variable aleatoria a pesar de que la respuesta sea toma café o no toma? Pues sí, y eso que la respuesta no es un número.
Y es que, podemos modificar la respuesta para que sí sea numérica. En estos casos, al éxito se le asigna el valor 1 y al fracaso el valor 0. Por tanto, tenemos una variable que tomará valores 0 y 1.
Además, a la probabilidad de éxito la vamos a llamar "p", con lo que la de fracaso será 1-p y la representaremos por la letra q.
 |
| Imagen de jgoge123 bajo licencia Creative Commons |
Una pregunta de un examen es de tipo test, consta de cuatro posibles respuestas pero no tenemos ni idea sobre la respuesta de la misma, así que la contestamos al azar. ¿Podemos definir una variable aleatoria sobre este experimento? ¿Cuáles serían la función de probabilidad, la media, la varianza y la desviación típica?
Un experimento aleatorio decimos que es de Bernoulli si sólo tiene dos posibles resultados al realizarse, a los que llamamos éxito y fracaso, según lo que estemos interesados. Una variable aleatoria basada en un experimento de Bernoulli tiene únicamente dos valores 0 y 1, asociados respectivamente al fracaso o al éxito de ese experimento de Bernoulli.
La probabilidad de éxito es el parámetro que define esta distribución y se representa mediante la letra p, y la función de probabilidad es entonces:
| xi |
pi |
| 0 | 1-p |
| 1 | p |
En cualquier distribución de Bernoulli las medidas representativas de centralización y dispersión vienen dadas en función de este parámetro y valen:
| Media | Varianza | Desviación Típica |
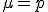 |
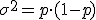 |
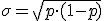 |
En la siguiente escena debes practicar sobre lo que acabamos de ver.
Son tres pantallas, en la primera debes decidir si un enunciado puede ser o no de Bernoulli, en la segunda calcular los valores del parámetro p y en la tercera todo lo que hemos visto.
 |
| Imagen en Wikimedia Commons bajo licencia Creative Commons |
Los Bernoulli (o Bernouilli) son una familia de matemáticos y físicos suizos procedentes de la ciudad de Basilea, que irrumpió en el mundo científico a finales del siglo XVII.
El fundador de esta familia fue Jacob el viejo, nacido en Amberes (Bélgica), un hugonote que se trasladó a Basilea en 1622 por motivos de persecución religiosa. Se casó tres veces y sólo tuvo un hijo, Nikolaus. Éste se casó y tuvo una docena, de los cuales cuatro llegaron a edad adulta; dos de ellos se convirtieron en matemáticos de primer orden: Jakob, nacido en 1654, y Johann, nacido en 1667. Ambos estudiaron la teoría del cálculo infinitesimal de Leibniz y desarrollaron aplicaciones de la misma.
Jakob Bernoulli (Basilea, 27 de diciembre de 1654 - 16 de agosto de 1705), también conocido como Jacob, Jacques o James Bernoulli, fue un matemático y científico. Siendo joven, su padre lo envió a la Universidad de Basilea para estudiar filosofía y teología, con el ánimo de que se convirtiera en teólogo. Pero Jakob continuó, a escondidas, las que eran sus auténticas aficiones la física y las matemáticas, según confiesa en su diario.
Su obra maestra fue Ars Conjectandi (el Arte de la conjetura), un trabajo pionero en la teoría de la probabilidad. La publicó su sobrino Nicholas en 1713, ocho años tras su muerte. Los términos ensayo de Bernoulli y números de Bernoulli son resultado de su trabajo. También existe un cráter en la Luna bautizado cráter Bernoulli en honor suyo y de su hermano Johann.