1.1. ¡Si casi todo es lo mismo!
 |
| Imagen de verino77 bajo licencia Creative Commons |
Vamos a seguir con los paralelismos entre estadística y probabilidad. Ya hemos visto que el significado de variable aleatoria o estadística es más o menos similar y que los tipos de variables son los mismos.
Si piensas un poco, recordarás que lo siguiente que hacíamos en estadística era ordenar los datos, hacer un recuento de los valores obtenidos, agruparlos e indicar el número de repeticiones de cada valor con la llamada frecuencia absoluta. Todo esto se solía colocar en una tabla ordenando de menor a mayor los valores y colocando al lado una columna con las frecuencias absolutas, ¿lo recuerdas? Además, si queríamos ver la representatividad de cada valor en el conjunto, construíamos una columna llamada frecuencia relativa cuyos valores salían de dividir cada frecuencia entre el total de datos.
Pues bien, con una variable aleatoria vamos a hacer algo muy similar, vamos a construir una tabla en la que vamos a colocar los valores que puede tomar la variable aleatoria X y al lado, no la frecuencia de ese valor, sino la probabilidad de que X tome ese valor, es decir, vamos a ir indicando los valores y las probabilidades de esos valores. Así, vamos a construir lo que se llama la Función de Probabilidad de la variable X.
 |
| Imagen de Daquellamanera bajo licencia Creative Commons |
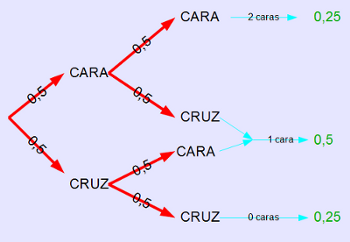
Blanca le propuso el siguiente juego a su amigo Gonzalo: Lanza 2 monedas y por cada cara que saques te doy 2€, ahora bien, si no sacas ninguna tú me darás 10 euros. Gonzalo por supuesto, aceptó el desafío.
¿Cuál es la función de probabilidad de este juego?
La función o distribución de probabilidad de una variable aleatoria discreta es la función que a cada valor xi de la variable le asocia su probabilidad pi.
P(X=xi) = pi
- La probabilidad pi es siempre no negativa y menor que 1: 0 ≤ pi ≤ 1.
- La suma de todas las probabilidades de los valores de la variable es 1.
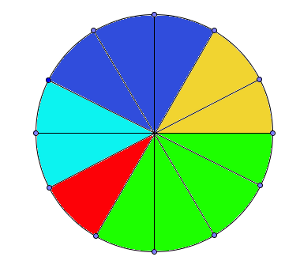 Observa la ruleta que tienes a la izquierda. Lanzamos una bola y según donde caiga ganamos una cantidad u otra de dinero. Si cae en el verde ganamos 1 €, si cae en el azul 3 €, si cae en el celeste 10 €, 15 si lo hace en el amarillo y por último 30 € si cae en la casilla roja.
Observa la ruleta que tienes a la izquierda. Lanzamos una bola y según donde caiga ganamos una cantidad u otra de dinero. Si cae en el verde ganamos 1 €, si cae en el azul 3 €, si cae en el celeste 10 €, 15 si lo hace en el amarillo y por último 30 € si cae en la casilla roja.
Definimos la variable aleatoria X = dinero ganado en la ruleta.
Completa en la siguiente tabla la función de probabilidad de esta variable aleatoria
| xi |
|||||
| pi |
|
|
|
|
|
Nota: Ordena los valores de X, que será el dinero ganado de menor a mayor, separa la parte entera de la decimal con "," y si es necesario, redondea a tres cifras decimales las probabilidades.
Y puestos a seguir recordando, seguro que te acordarás de la media, de la varianza, ... Estos eran los llamados parámetros estadísticos y servían para resumir toda la información que nos aportaba la muestra. Había muchos parámetros, y todos tienen su equivalente en una función de probabilidad, pero vamos a conformarnos con los tres más representativos, la media, la varianza y la desviación típica.
En el siguiente ejemplo vamos a ver cómo se calculan estas tres medidas a partir de los mismos datos del ejemplo anterior.
La media o esperanza matemática de una variable aleatoria, se expresa con la letra griega 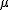 y se calcula sumando los productos de cada valor por su probabilidad:
y se calcula sumando los productos de cada valor por su probabilidad:
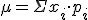
La varianza, que se expresa por 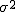 se calcula sumando los productos del cuadrado de cada valor por su probabilidad y restarle a esta suma el cuadrado de la media:
se calcula sumando los productos del cuadrado de cada valor por su probabilidad y restarle a esta suma el cuadrado de la media:
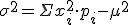
Por último, la desviación típica  , se calcula hallando la raíz cuadrada de la varianza.
, se calcula hallando la raíz cuadrada de la varianza.
Un juego de azar se considera justo cuando la ganancia media que se espera obtener es 0 €, o sea, cuando el dinero que arriesgas, el premio que recibes y las probabilidades de ganar o perder van equiparadas.
Puedes comprobar que la mayoría de los juegos de azar, loterías, quinielas, rifas, etc, no son justos.
Una variable aleatoria discreta tiene la siguiente función de probabilidad:
| xi | 0 |
1 |
2 |
3 |
4 |
| pi | 0,4 | 0,1 | 0,15 |
0,25 |
0,1 |
La media es ; la varianza y la desviación típica
(Separa la parte decimal con "," y en la desviación típica pon tres decimales)
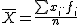 . Pero si te fijas, si dividimos cada frecuencia por el total de datos, estamos dando la probabilidad de que ocurra el valor xi. Por tanto, lo que hemos de hacer es multiplicar cada valor por su probabilidad y sumar todos los productos:
. Pero si te fijas, si dividimos cada frecuencia por el total de datos, estamos dando la probabilidad de que ocurra el valor xi. Por tanto, lo que hemos de hacer es multiplicar cada valor por su probabilidad y sumar todos los productos:
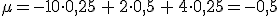
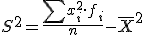 . Pues bien, igual que antes, si sustituimos esas frecuencias entre el número de datos por la probabilidad del valor, vemos que tenemos que multiplicar el cuadrado de cada valor de X por su probabilidad, sumar todos los productos y restarle la media al cuadrado.
. Pues bien, igual que antes, si sustituimos esas frecuencias entre el número de datos por la probabilidad del valor, vemos que tenemos que multiplicar el cuadrado de cada valor de X por su probabilidad, sumar todos los productos y restarle la media al cuadrado.
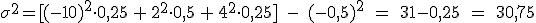
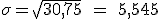 €
€