2.2. ¡Feliz cumpleaños compartido!
Después de un día tan ajetreado en Sanlúcar de Barrameda, nuestros amigos cogieron el coche de regreso a Mérida, en Extremadura, ya que iban a celebrar el cumpleaños de un amigo que conocieron en Trujillo pero ahora vivía en esta preciosa ciudad de Mérida.

|
| Imagen de Mates y Más bajo licencia Creative Commons |

|
| Imagen de Dan perry bajo licencia Creative Commons |
Durante el viaje, Blanca comentó, que la amiga de M.ª José le había dicho en un momento de la tarde, que la probabilidad era mentira, porque tenías unos amigos aficionados al golf y cada vez que los veía jugar, comprobaba lo difícil que era meter la pelota en el agujero, pero sin embargo la probabilidad, según ella era del 50 %, o la metía o la tiraba fuera.
Gonzalo empezó a dudar, pero rápidamente M.ª José los sacó de dudas.
Existe una regla en probabilidad que se llama Regla de Laplace, que nos dice que la probabilidad de que ocurra un suceso es igual al cociente entre el número de casos favorables y el número de casos posibles, pero...
Blanca la interrumpió diciéndole, eso es. Si consideramos el suceso "meter la bola con un lanzamiento", los casos posibles son 2, meterla o fallar y los casos favorables son 1, meterla, luego la probabilidad es 1/2.
Entonces M ª José le dijo que la dejara terminar.
La regla de Laplace sólo es válida cuando los sucesos son equiprobables, es decir, cuando tienen la misma probabilidad de que ocurran, y en este caso, para que fueran equiprobables, tendríamos que llenar el campo de golf de agujeritos del tamaño del agujero principal y considerar el agujero donde está el banderín como 1 entre muchos, con lo cual no son equiprobables los sucesos meter la bola en un agujerito pequeño y colocar la bola en el resto del campo que imaginariamente estaría formado por multitud de agujeritos del mismo tamaño. Y no se puede aplicar esta regla.
Gonzalo se puso muy contento y le dijo a M.ª José, por fin lo he entendido.
Cuando ya estaban llegando a su destino, M.ª José les dijo a sus amigos, que en el cumpleaños de sus amigos, que iban a ir 40 personas, casi seguro que habría otra persona allí que cumpliera los años también ese día, ya que había una probabilidad de más del 90% de que esto ocurriera.
Compruébalo cuando estés con un grupo de más de 30 personas.
En este último apartado del tema, recordaremos como utilizar la probabilidad para resolver problemas, siempre analizando previamente si los sucesos son equiprobables o no.
Regla de Laplace:
Si un espacio muestral está formado por un número finito de sucesos simples y todos ellos tienen la misma posibilidad de suceder, entonces la probabilidad de un suceso A es el cociente entre el número de casos favorables al suceso A y el número de casos posibles.
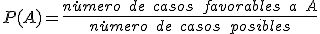
Los casos posibles son todos los resultados del experimento, es decir, todos los elementos del espacio muestral y los casos favorables son los elementos del suceso A.
En casos como el lanzamiento de una chincheta, o cuando un dado está mal construido, los sucesos no son equiprobables, no se puede utilizar la regla de Lapalce y hay que recurrir a la Ley de los grandes números.

|
| Imagen de Bananaguay bajo licencia Creative Commons |
Calcula las siguientes probabilidades. Escribe el resultado en decimales utilizando la coma.
1. Experimento: sacar una carta de una baraja española de 40 cartas.
Sucesos: A="salir As" , B="salir figura", C="salir espadas"
a) P(A)=
b) P(B)=
c) P(C)=
d)P(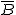 )=1-
=
)=1-
=
2. Experimento: Lanzar dos dados cúbicos numerados del 1 al 6.
Sucesos: A="la suma de las caras superiores es 7" , B="Los números de las dos caras superiores son primos"
a) P(A)= /36.
b) P(B)= /36.
En esta página creada por José Luis Álvarez García y Rafael Losada Liste, podrás conocer un poco más del famoso problema propuesto por el Conde de Buffon.
¿Qué tiene que ver la aguja de Buffon, con la probabilidad y con el número π?

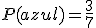 ;
;  ;
;