2.1. Tuenti o Twitter
 |
| Imagen de Cirofono bajo licencia Creative Commons |
En el juego anterior hablamos de qué tarjeta elegir para que tuviéramos mayor probabilidad de ganar el coche.
Recuerda del curso pasado que la probabilidad de que ocurriera un suceso se medía con un número comprendido entre 0 y 1, que si estaba cerca de 1 era más probable y cerca de 0, menos probable.
En la partida de dados de nuestros amigos de la Peña "Los improbables", M.ª José era la que tenía más posibilidades de ganar (mayor probabilidad), seguramente porque era la matemática y jugaba con ventaja, y la amiga de M.ª José era la que tenía más probabilidad de perder.
Gonzalo y Blanca tenían las mismas posibilidades, aunque menor que Mª José.
¿Por qué crees que ocurría esto?
Espero que a partir de ahora, si todavía no te has dado cuenta, seas consciente de lo importante que es saber matemáticas, al menos para que no te tomen el pelo.
Actividad
Recuerda que llamamos probabilidad de un suceso A, al nivel de certeza que tenemos de que ocurra dicho suceso y esto se mide con un número comprendido entre 0 y 1.
 |
| Imagen de Juan Pérez Rosales bajo licencia Creative Commons |
Volvamos a la partida de dados de nuestros amigos.
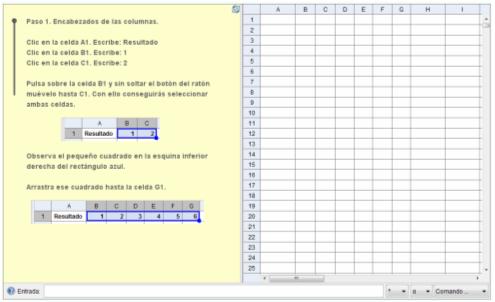
En la siguiente escena de GeoGebra creada por José Luis Álvarez García y Rafael Losada Liste, puedes hacer una simulación del lanzamiento de mil dados cúbicos con números del 1 al 6, o lo que es lo mismo el lanzamiento de un dado mil veces.
Practica con ella e intenta responder a la pregunta que te hacía al principio de este apartado, sobre la probabilidad que tenía cada jugador de ganar.
Haz clic en la imagen.
Ejemplo o ejercicio resuelto
|
| Imagen de Rennett Stowe bajo licencia Creative Commons |
Supongamos que tomamos los resultados que vienen en el ejemplo de la escena de GeoGebra anterior. En mil lanzamientos, estas son las veces que han salido cada número:
| Número | 1 |
2 |
3 |
4 |
5 |
6 |
| Número de veces |
173 | 186 |
167 | 156 |
171 | 147 |
Si consideramos el suceso S="salir el 1"={1}, tenemos que ha salido 173 veces, o lo que es lo mismo, que su frecuencia absoluta es 173.
Como hemos lanzado el dado 1000 veces, tenemos que la frecuencia relativa de S es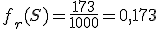
.
a) ¿Cuál es la frecuencia relativa de "salir el 3"?
b) Si consideramos los sucesos de la partida de nuestros amigos:
A="Salir un número impar" (ganaba Gonzalo); B="Salir un número primo" (ganaba Blanca); C="Salir un divisor de 6"(ganaba M.ª José), D="Salir un múltiplo de 4" (ganaba la amiga de M.ª José).
¿Cuál es la frecuencia relativa de cada uno de los sucesos?
c) ¿Es cierto que Mª José tiene más posibilidades de ganar?
d) En este caso, ¿tienen las mismas posibilidades Gonzalo y Blanca de ganar? ¿Cuándo tendrían la misma posibilidad?
.
.
Actividad
Recuerda que llamamos frecuencia absoluta de un suceso S, y la representamos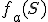 
, al número de veces que ocurre dicho suceso.
Llamamos frecuencia relativa de un suceso S, y la representamos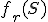 
,al cociente de la frecuencia absoluta entre el número de veces, n, que se ha repetido el experimento, es decir 
.
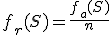Cuando el número de pruebas que hacemos de un experimento crece indefinidamente, la frecuencia relativa de un suceso tiende a estabilizarse en un número, que es la probabilidad del suceso. Este resultado es lo que llamamos Ley de los grandes números.
La probabilidad de un suceso S suele representarse por P(S) y tiene las siguientes propiedades:
- La probabilidad de un suceso es siempre un número comprendido entre
0 y 1:
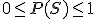. - La probabilidad del suceso seguro es 1 y la del suceso imposible
es 0:
, 
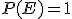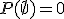. - La suma de las probabilidades de los sucesos elementales vale 1.
- La suma de un suceso y de su suceso contrario vale 1:
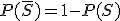. - La probabilidad de un suceso es igual a la suma de las probabilidades de los sucesos elementales que lo forman.
Objetivos
En el siguiente enlace puedes comprobar la Ley de los grandes números y en la pestaña superior "Ejercicios" puedes practicar con problemas de probabilidad.
Actividad
Unión de sucesos:
Si A y B son sucesos compatibles, la probabilidad de la unión es: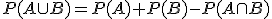 
.
AV - Actividad de Espacios en Blanco
 |
| Imagen de Jesús León bajo licencia Creative Commons |
En una encuesta realizada entre el alumnado de 2º de Bachillerato de un instituto, el 80% utiliza la red social "Tuenti" y el 20% utiliza "Twitter".
Además, el 15% utiliza Tuenti y Twitter. ¿Con estos datos, cuál es la probabilidad de que un estudiante, elegido al azar, utilice Tuenti o Twitter?
Llamamos TU al suceso "utilizar Tuenti" y TW al suceso "utilizar Twitter".
Las probabilidades que no da el problema son:
P(TU)=0,8; P(TW)= y P(TU ∩ TW)= .
El problema nos pide P(TU 
TW)=P(TU) + P(TW) - P(TU ∩ TW)=
+
-
=
.
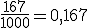
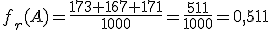
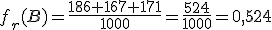
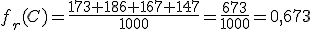
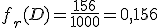
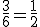