1.2. ¿Habrá que aplicar las derivadas, no?
 |
| Imagen de eltiempo.com bajo licencia Creative Commons |
Ya tenemos claro cómo hay que plantear el problema, pero claro, hay que resolverlo porque si no, a ver qué estamos haciendo. Pues eso es lo que vamos a ver en este apartado del tema, cómo calcular la solución, aunque en realidad, en este apartado no vamos a dar todavía con la solución, sino con los valores candidatos a solución.
En el segundo tema de esta unidad, vimos que los máximos y mínimos relativos, si la función era continua, se alcanzaban en los puntos donde la función cambiaba de creciente a decreciente o de decreciente a creciente respectivamente. Pero claro, sería una lata tener que ver toda la monotonía de la función cuando en realidad sólo nos interesa el punto donde se produce el cambio.
En ese tema has visto que los extremos relativos se alcanzan en los puntos donde la primera derivada es cero, así que eso es lo que vamos a hacer para buscar los puntos candidatos a máximo o mínimo, calcular la primera derivada, igualarla a cero y resolver la ecuación que resulte.
Otra cosa será ya ver si es o no la solución, pero al igual que unas elecciones, hay que empezar conociendo a los candidatos para elegir después al ganador.
Los valores candidatos a ser solución de un problema de optimización se obtienen derivando la función, igualando a cero la derivada y resolviendo la ecuación.
Esos valores se llaman puntos críticos de la función.
Verdadero Falso
2) El consumo de un barco según la velocidad x, viene dado por la función 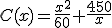 . Para determinar los extremos relativos tenemos que resolver la ecuación:
. Para determinar los extremos relativos tenemos que resolver la ecuación:
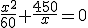
Verdadero Falso
Verdadero Falso
