1.1. Lo primero, entablar relaciones
 |
Sabes, quizás esta aventura de Martín en busca del chiringuito es demasiado complicada de resolver para empezar. Vamos a fijarnos en otra situación a la que también tiene que hacer frente Martín, esta vez en compañía de su amigo Felipe, para explicar de forma clara cómo se resuelven estas cuestiones.
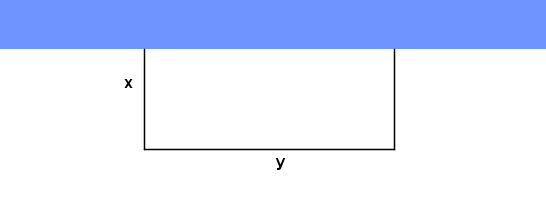
La finca que regentan, "La Alfonsita", tiene una zona donde el límite es un arroyo. Pues bien aprovechando ese límite, quieren vallar un trozo de tierra para sembrar lechugas y coles y con el fin de que las cabras no puedan entrar. Para aprovechar mejor el terreno, quieren que esa parcela sea rectangular, y claro, el lado que linda con el arroyo no habría que vallarlo. Además, en una nave tienen guardado un rollo de valla de aproximadamente 300 metros y estiman que con esa cantidad es suficiente para el terreno que quieren dedicar a las lechugas y coles
Y ahora la pregunta que le surge a Martín y a Felipe es: -vale, podemos hacer que la forma sea un rectángulo, pero podemos construir muchos rectángulos con esta valla, más ancho o más estrecho, pero... ¿con cuál cubriremos más cantidad de tierra?
Martín no lo dudo:-no te preocupes, le pregunto a mi amiga Alba. Pero Alba no tenía el móvil disponible, así que, ¿le puedes contestar tú?
Para empezar tenemos que buscar algo a lo que buscarle el máximo o el mínimo. En este caso, lo que queremos es que la valla abarque la máxima cantidad de tierra, y eso lo que quiere decir es que el área que ocupe la parcela vallada sea la máxima posible.
Así que, ya tenemos claro lo que queremos, que el área de la parcela sea máxima.
Ahora tenemos que expresar eso con una función. ¿Cómo lo hacemos?
Para resolver un problema de optimización, lo primero es construir la función a maximizar o minimizar, y conseguir que esta dependa de una sola variable.
Si en el contexto del problema aparecen más de una variable, habrá que buscar alguna relación entre ellas de entre los datos que nos aporte el problema. Una vez encontrada esta relación, se tiene que despejar y sustituir en la función para que esta sí dependa ya de una sola variable.
Verdadero Falso
Verdadero Falso
Verdadero Falso