4.1. Ionah ed serrot sal
 |
| Imagen de AnsiaPerenne bajo licencia Creative Commons |
Verdadero Falso
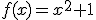 y
y
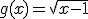
Verdadero Falso
Tanto hablar de funciones inversas, ¿para qué?
¿Te acuerdas de lo que eran los logaritmos? Seguro que sí, porque es algo de lo que cualquier estudiante con el paso del tiempo siempre se pregunta para qué sirven.
Te recuerdo que el logaritmo de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número.
Por ejemplo, el logaritmo con base b de un número x es el exponente n al que hay que elevar esa misma base para que nos dé dicho número x.
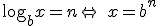
La base b tiene que ser positiva y distinta de 1. 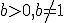 . x tiene que ser un número positivo (x > 0).
n puede ser cualquier número real(
. x tiene que ser un número positivo (x > 0).
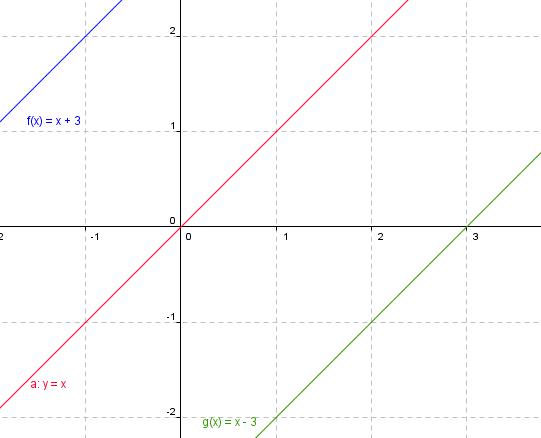
n puede ser cualquier número real( ).
).
Pero lo mejor para entender el concepto de logaritmo es que disfrutes con este vídeo de dos genios como son Ismael Roldán y Pepe Muñoz.
Vídeo subido a YouTube por humormates.
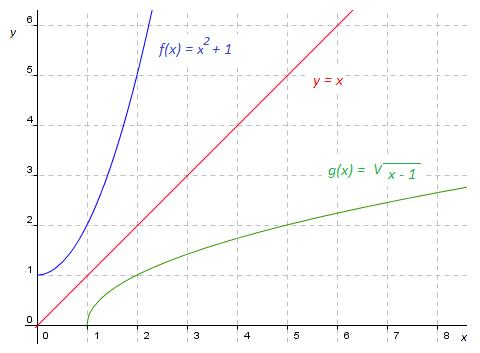
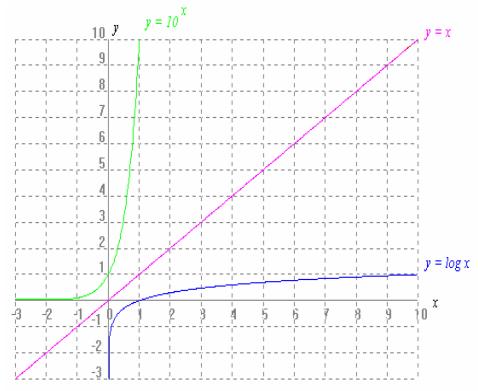
Comprueba utilizando la definición que las funciones f(x)=10x y g(x)=logx, son funciones inversas.
Basándote en la simetría de dos funciones inversas, representa g(x).
¿Se le puede dar a x valores negativos?, ¿y el valor 0?
Estudia el dominio, crecimiento y puntos de corte con los ejes de coordenadas de g(x).
¿Qué ocurre cuando la x toma valores muy pequeños (positivos)?
La función logarítmica y=logx es una función continua creciente en todo su dominio, que es el conjunto de los números reales positivos. Corta al eje OX en el punto (0,1) y para valores de x próximos a cero la función toma valores negativos muy grandes.
En la siguiente animación del Banco de imágenes y sonidos del ITE, puedes practicar representando gráficas de funciones logarítmicas.
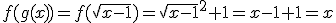 .
.