1. La importancia de ser afín
Nuestros amigos de la caseta de TRANS VELOX, descubren día a día, como situaciones cotidianas se reflejan en una gráfica de forma lineal: el dinero que se obtiene en función del número de tickets de comida y bebida que se venden, el número de botellas de manzanilla que se compran en función del coste de cada una, etc.
 |
| Imagen de Dave_McLean bajo licencia Creative Commons |
El primer tipo de función que vamos a recordar es la función afín, cuya representación gráfica es una recta o un conjunto de puntos alineados, dependiendo de si la variable con la que estamos trabajando es continua o discreta respectivamente.
En el caso del número de tickets y el número de botellas de manzanilla, como toman valores concretos, estaríamos hablando de variables discretas.
Ejemplo o ejercicio resuelto
Aprovechando que la caseta está a tope, Nacho ha traído unas papeletas para venderlas y sacar dinero para irse de campamento de verano con su grupo scout.
 |
| Imagen de david-gilmour bajo licencia Creative Commons |
Nacho ha conseguido ganar en un mes 20 euros vendiendo bombones y ahora vende estas papeletas obteniendo un beneficio de 2 € por cada papeleta vendida.
Si x es el número de entradas e y el dinero que tiene Nacho, ¿qué expresión relaciona x con y?
Construye una tabla de valores y representa la gráfica correspondiente.
¿Se trata de una función lineal? ¿Por qué?
¿Cuál es el dominio de definición de la función?
Si Nacho consigue vender 30 papeletas, ¿cuánto dinero tendrá, en total, para el campamento?
En la siguiente animación del Banco de imágenes y sonidos del ITE, puedes practicar representando gráficas de funciones afines de variable continua.
Actividad
Una función afín es aquella cuya expresión analítica es de la forma y=mx+n, y su gráfica es una recta o un conjunto de puntos alineados, que pasa por el punto (0,n).
La constante m es la pendiente de la función y la constante n es la ordenada en el origen.
Una función lineal es un caso particular de función afín (n=0).
AV - Reflexión
A Alejandro, uno de los nietos del gerente de TRANS VELOX le encanta montarse en los coches de choque.
 |
| Imagen de guillermocandao bajo licencia Creative Commons |
El sábado de feria se organizó un campeonato en la pista más grande del recinto ferial.
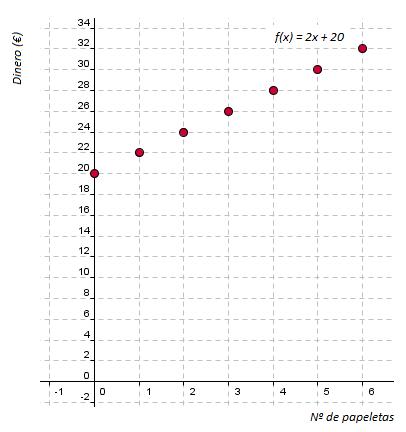
La prueba consiste en dar 9 vueltas a la pista en el menor tiempo posible. Cada vuelta tiene 100 metros de longitud.
Alejandro realiza la primera vuelta al circuito a una velocidad constante de 9 km/h, y así sigue hasta dar las 9 vueltas que hacen falta para llegar a la meta.
- ¿Cuánto tardará en dar 4 vueltas?
- ¿Cuánto tiempo tardará en llegar a la meta?
- Cinco minutos después de tomar la salida, ¿cuántas vueltas lleva Alejandro?
- Si llamamos x al número de vueltas e y al tiempo empleado, ¿qué expresión analítica relaciona x con y?
- Dibuja la gráfica correspondiente a la expresión anterior.
.
Actividad
La gráfica de esta función es una recta que pasa por el origen, es un ejemplo de función de proporcionalidad directa o función lineal.
Su expresión analítica es de la forma y=m·x, siendo m la constante de proporcionalidad.
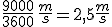