2.1 Ayudado por los vectores
|
Dados varios vectores
Por ejemplo, si en el espacio vectorial |
 |
| Brújula. Imagen obtenida del Banco de imágenes del ITE |
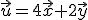 , y
, y 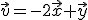
Se dice entonces que los vectores
 y
y 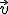 son combinación lineal de
son combinación lineal de 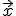 e
e 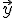 . Que es lo mismo que decir que
. Que es lo mismo que decir que  lo podemos poner como combinación lineal de
lo podemos poner como combinación lineal de 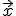 y
y 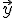 y lo mismo con
y lo mismo con 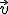
Veamos cómo:
1.- Cambia el valor de n a n=4. Así se obtiene el vector
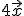
2.- Cambia el valor de m a m=2. Así se obtiene el vector
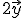
3.- Arrastra el punto B, trazando una paralela al vector
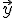
4.- Arrastra el punto C, trazando una paralela al vector
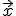
5.- Prolongando estas paralelas suficientemente obtienes un paralelogramo cuyos lados son los vectores
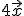 y
y 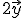 . Arrastra el punto A para dibujar la diagonal que representa al vector
. Arrastra el punto A para dibujar la diagonal que representa al vector 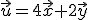
6.- Ahora le das a n = -2 para dibujar el vector
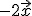 y a m=1 para dibujar el vector
y a m=1 para dibujar el vector 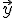
7.- Arrastra el punto D, trazando una paralela al vector
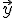
8.- Arrastra el punto E, trazando una paralela al vector
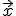
9.- Prolongando estas paralelas suficientemente obtienes una paralelogramo cuyos lados son los vectores
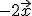 e
e 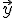 . Arrastra el punto A, de nuevo, para dibujar la diagonal que representa al vector
. Arrastra el punto A, de nuevo, para dibujar la diagonal que representa al vector 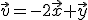
Probemos ahora en 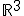 . Dado los vectores
. Dado los vectores 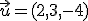 ,
, 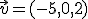 y
y 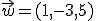 indica el vector que se obtiene como combinación lineal en cada uno de los siguientes casos. Para ello te proporcionamos el...
indica el vector que se obtiene como combinación lineal en cada uno de los siguientes casos. Para ello te proporcionamos el...
Centro de operaciones con vectores en el espacio de tres dimensiones
1.- 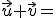
2.- 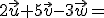
3.- 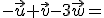
4.- 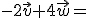
5.- 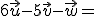
Practica con otras combinaciones lineales que desees seleccionando otros vectores.
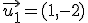 y
y 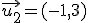 , el vector
, el vector 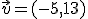 lo podemos poner como combinación lineal de los dos anteriores dos. Inténtalo a ver cómo lo harías.
lo podemos poner como combinación lineal de los dos anteriores dos. Inténtalo a ver cómo lo harías.
Te proponemos ahora una actividad parecida a la anterior pero en el espacio de tres dimensiones  . Dados los vectores
. Dados los vectores 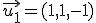 ,
, 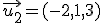 y
y 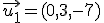 escribe el vector
escribe el vector 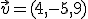 como combinación lineal de los tres anteriores. Realiza los cálculos y asegúrate de los mismos utilizando la siguiente ventana.
como combinación lineal de los tres anteriores. Realiza los cálculos y asegúrate de los mismos utilizando la siguiente ventana.
|
Combinación lineal de vectores en el espacio vectorial de tres dimensiones. Escribe en la primera columna el primer vector, en la segunda el segundo y en la tercera el tercer vector. Escribe en la cuarta columna el vector que desees poner como combinación lineal de los dos anteriores. Los valores A, B y C que aparecen al pulsar en resolver son la combinación lineal pedida
|
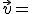
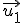
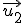
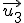
Dados varios vectores  ,
, 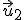 , ...
, ...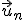 de un espacio vectorial, decimos que son linealmente independientes si al resolver la ecuación:
de un espacio vectorial, decimos que son linealmente independientes si al resolver la ecuación:
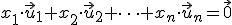
donde 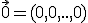 es el vector nulo, tenemos como única solución
es el vector nulo, tenemos como única solución 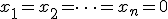
Tratemos de simplificar esta definición a través de algunos ejemplos
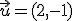 y
y 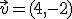 , comprueba si son linealmente independientes
, comprueba si son linealmente independientes
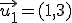 , , 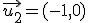 y y 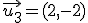
| |
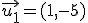 y y 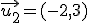
| |
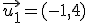 y y 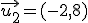
| |
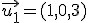 y y 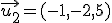
| |
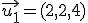 , , 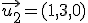 y y 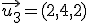
| |
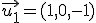 , , 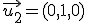 y y 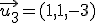
| |
 de un espacio vectorial y dados varios números
de un espacio vectorial y dados varios números 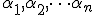 se denomina combinación lineal al vector que resulta de hacer las siguientes operaciones:
se denomina combinación lineal al vector que resulta de hacer las siguientes operaciones: 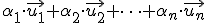 .
.
 consideramos los vectores
consideramos los vectores 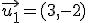 y
y 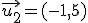 , una combinación lineal podría ser
, una combinación lineal podría ser 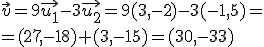
 y
y  de forma que
de forma que 
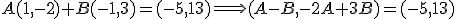
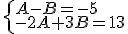 El rango de la matriz de coeficientes es 2, que es el mismo que el número de incógnitas y de ecuaciones, por lo que el sistema es compatible determinado, tiene una solución que la obtenemos por el método de Gauss multiplicando la primera fila por 2 y sumándosela a la segunda:
El rango de la matriz de coeficientes es 2, que es el mismo que el número de incógnitas y de ecuaciones, por lo que el sistema es compatible determinado, tiene una solución que la obtenemos por el método de Gauss multiplicando la primera fila por 2 y sumándosela a la segunda:
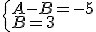 Luego
Luego 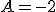 y
y 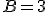
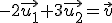
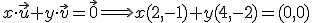
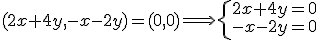
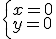 pero tenemos que ver si es la única. Para ello tenemos que ver el rango de la matriz de coeficientes del sistema de ecuaciones. Calculamos el determinente de esta matriz
pero tenemos que ver si es la única. Para ello tenemos que ver el rango de la matriz de coeficientes del sistema de ecuaciones. Calculamos el determinente de esta matriz
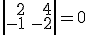
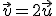 por lo que
por lo que