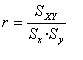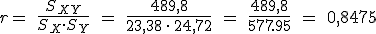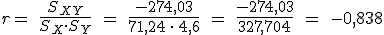1.2 Relaciones positivas y negativas.
Ejemplo o ejercicio resuelto
 |
Uno de los estudios estadísticos medioambientales que Mercedes realizó, trataba sobre la calidad de las aguas de baño de carácter marítimo en la comunidad de Andalucía. Entre otros muchos aspectos, se contabilizaba el número de playas por provincias y el número de puntos costeros en dichas provincias en las que el agua tenía una calificación de "Buena".
Los datos obtenidos son los que se recogen en esta tabla:
| Provincia |
Almería | Cádiz | Granada |
Huelva |
Málaga |
| N.º de playas |
68 | 44 | 28 |
15 |
77 |
|
N.º de puntos con calificación "buena" |
82 | 52 | 16 | 44 | 81 |
Mercedes piensa que el hecho de que haya playas influye decisivamente en el tratamiento de las aguas y hace que haya muchos puntos en la costa con calificación "buena".
¿Tendrá razón?
Ejemplo o ejercicio resuelto
 |
| 6. Imagen de Histerica Sweet bajo licencia Creative Commons |
Una de las enfermedades que más preocupó y más alarma social creó desde finales de los 80 y la década de los 90 fue el Sida, por lo desconocido, por la inexistencia de medicamentos y vacunas para la enfermedad y por la serie de personalidades famosas de todos los ámbitos que sucumbieron ante dicha enfermedad.
Pues bien, en otra de las estadísticas hospitalarias que Mercedes estaba manejando, se analizaba el comportamiento de esta enfermedad en la provincia de Sevilla. En la siguiente tabla, se muestra el número de casos producidos en la provincia desde el año 92 hasta 2007.
| Año | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 |
2002 | 2003 |
2004 |
2005 |
2006 |
2007 |
| Casos | 141 | 187 | 266 | 273 | 220 | 175 | 140 | 138 | 98 | 111 | 96 | 95 | 67 | 74 | 50 | 22 |
De manera evidente se ve que el número de casos ha ido disminuyendo a lo largo de los años salvo algunos repuntes, pero, ¿este comportamiento es regular o es un poco aleatorio?
Pues para contestar a esto, Mercedes calculará nuevamente el coeficiente de correlación lineal.
Pre-conocimiento
AV - Pregunta de Elección Múltiple  |
| 7. Imagen de castisoto bajo licencia Creative Commons |
Vamos a resolver la siguiente situación realizando todos los pasos que hemos visto en los ejemplos resueltos:
En una cofradía de pescadores, las capturas registradas de sardinas, en kilogramos, y el precio de subasta en la lonja, en €/kg, fueron los siguientes:
| Sardinas (kg) | 2000 | 2400 | 2500 | 3000 | 2900 | 2800 | 3160 |
| Precio (€/kg) | 1,80 | 1,68 | 1,65 | 1,32 | 1,44 | 1,50 | 1,20 |
¿Qué relación existe entre el número de kilos capturados y el precio de venta en la lonja?
1) La media de los kilos de sardinas capturados es:
|
3126 kg
| |
|
3024 kg
| |
|
2680 kg
|
|
269,07 kg
| |
|
46,74 kg
| |
|
-398,4 kg
| |
|
372,02 kg
|
|
1,49 €/kg
| |
|
1,51 €/kg
| |
|
1,53 €/kg
| |
|
1,55 €/kg
|
|
0,19 €/kg
| |
|
-0.19 €/kg
| |
|
2,21 €/kg
| |
|
-2,21 €/kg
|
|
60,78
| |
|
269,07 kg
| |
|
-142,678
| |
|
-70,88
|
|
Fuerte
| |
|
Muy fuerte
| |
|
Débil
| |
|
Muy débil
|
Para saber más
 |
| 8. Imagen de Fastfission en Wikimedia Commons bajo licencia Creative Commons |
Sir Francis Galton (16 de febrero de 1822 – 17 de enero de 1911). Antropólogo, geógrafo, explorador, inventor, meteorólogo, estadístico y psicólogo británico.
No tuvo cátedras universitarias y realizó la mayoría de sus investigaciones por su cuenta. Sus múltiples contribuciones recibieron reconocimiento formal cuando, a la edad de 87 años, se le concedió el título de Sir o caballero del Reino.
De intereses muy variados, Galton contribuyó a diferentes áreas de la ciencia como la psicología, la biología, la tecnología, la geografía, la estadística o meteorología. A menudo, sus investigaciones fueron continuadas dando lugar a nuevas disciplinas.
Primo segundo de Charles Darwin, aplicó sus principios a numerosos campos, principalmente al estudio del ser humano y de las diferencias individuales.
En el campo de la estadística, la principal contribución de Galton fue el concepto de correlación entre pares de atributos, aplicándolo a problemas sobre herencia y genética.