1.1 El medidor de relaciones
 |
| 5. Imagen de Chistian Frausto Bernal bajo licencia Creative Commons. |
Bueno, pues ahora que ya sabemos calcular la covarianza, estamos en condiciones de calcular ese indicador que nos diga a modo de termómetro cuánto de fuerte o débil es el grado de dependencia entre las variables, y este indicador se llama coeficiente de correlación lineal.
La relación o dependencia entre las variables podemos buscarla de muchas formas, pero vamos a centrarnos en estudiar la dependencia lineal, esto es, averiguar si los datos que me están dando podrían ajustarse al comportamiento que tendría una función lineal o afín, y para ello vamos a usar este coeficiente.
El coeficiente de correlación lineal de Pearson, que representamos con la letra r, es una medida de la variable (X,Y) que determina el grado de dependencia lineal entre las variables X e Y. Se calcula usando la expresión:
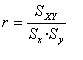
donde SXY indica la covarianza de la variable (X,Y), SX la desviación típica de X y SY la desviación típica de Y.
En la siguiente escena puedes comprender mejor el significado del coeficiente de correlación lineal. Aparecen doce puntos que puedes mover libremente por toda la escena con el ratón. En cada movimiento que hagas te aparecerá el valor del coeficiente de correlación lineal de Pearson.
Applet Descartes de Luis Barrios Calmaestra bajo licencia Creative Commons.
Contesta a las siguientes cuestiones manipulando los puntos que aparecen en la escena.
- Coloca los puntos en una línea recta creciente ¿Cuánto vale el coeficiente de correlación lineal?
- Separa poco a poco los puntos de la línea recta, ¿qué ocurre con r?
- Coloca los puntos en una línea recta decreciente ¿Cuánto vale el coeficiente de correlación lineal?
- Separa poco a poco los puntos de la recta y observa como se aleja de -1 el valor de r.
- Intenta distribuir los puntos de forma que el coeficiente de correlación lineal valga 0. Explica qué tiene que pasar para que dicho coeficiente valga 0.
- Coloca los puntos intentando construir una parábola. ¿Cuánto vale el coeficiente de correlación lineal?
Como has visto, el coeficiente de correlación lineal siempre se mueve entre -1 y 1. El valor podemos interpretarlo de la siguiente forma:
| Si r = 1 ó -1, la dependencia entre las variables es funcional, es decir, la relación es perfecta pues obedece a una función. | |
|
Si 0,85<r<1, correlación positiva y muy fuerte. Si 0,7<r<0,85 correlación positiva y fuerte Si 0,5<r<0,7 correlación positiva media Si 0,3<r<0,5 correlación positiva débil Si 0<r<0,3, correlación positiva muy débil |
Si -1<r<-0,85 correlación negativa y muy fuerte Si -0,85<r<-0,7 correlación negativa y fuerte Si -0,7<r< -0,5 correlación negativa media Si -0,5<r<-0,3 correlación negativa débil Si -0,3<r<0 correlación negativa muy débil |
| Si r = 0, no existe correlación lineal. En este caso decimos que las variables están incorreladas. |
|
Ojo:
Si dos variables son incorreladas, no tienen necesariamente que ser independientes, pues incorrelada significa que no existe relación lineal pero no quita que exista una dependencia curvilínea. Sin ir más lejos, en la sexta pregunta de la autoevaluación, habrás podido observar que el coeficiente de correlación es 0 ( variables incorreladas) pero existe una relación funcional que obedece a una función cuadrática, así que, de independientes, nada de nada.
Al revés sí se cumple. Si dos variables son independientes, seguro que son incorreladas, pues al no haber ningún tipo de relación, seguro que tampoco hay la lineal.
Existe otro coeficiente, llamado coeficiente de determinación, que se representa por R2 y se calcula como el coeficiente de correlación al cuadrado.
Este coeficiente toma siempre valores entre 0 y 1 y tiene la enorme ventaja de que multiplicado por 100, nos indica el tanto por ciento de relación existente entre las variables.
Por ejemplo, si hemos obtenido un coeficiente de correlación r = 0,941, el coeficiente de determinación es R2 = 0,9412 = 0,8855; o sea, que la dependencia entre las variables es del 88,55%, bastante fuerte por tanto.