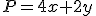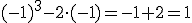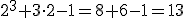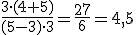1.3. Los números dan vida a las letras
 |
| math nerds on 4th street de auralninja, CC by-nc-sa 2.0 |
En este apartado nos vamos a centrar en las fórmulas. La que tienes en la imagen es la fórmula para resolver una ecuación de segundo grado. Pero eso lo trataremos más adelante...
Las primeras fórmulas con las que se suele trabajar en matemáticas son las geométricas. Podemos calcular la superficie o el perímetro de una figura aplicando fórmulas que ya conocemos.
Recuerda que la superficie de un cuadrado es la medida del lado elevado al cuadrado, y la del rectángulo es igual a la base por su altura. El perímetro de una figura es la suma de todos los lados.
Teniendo estos datos, podemos calcular una fórmula para la superficie de la siguiente habitación:
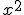
- La parte rectangular tiene superficie 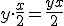
- Uniendo ambas, tenemos la superficie de la habitación: 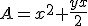
- El perímetro será: 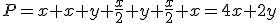
Una vez que tenemos una fórmula, podemos utilizarla para averiguar cuánto valen al cambiar los valores de las variables. A esto lo llamamos valor numérico de una expresión algebraica.
En nuestro caso, podríamos averiguar la superficie y el perímetro de la habitación tanto en el caso de que sea una maqueta como si fuese una casa real, sustituyendo el valor de las variables en la fórmula. Veamos un par de ejemplos:
| Variables |
Superficie
|
Perímetro
|
|
x = 5 cm y = 8 cm |
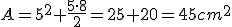 |
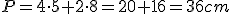 |
|
x = 2,5 m y = 4 m |
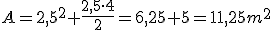 |
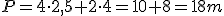 |
Puedes encontrar más fórmulas de figuras geométricas en este enlace.
Vamos a buscar una fórmula que me diga el número de cerillas que necesito para formar los siguientes triángulos. Es parecido al ejemplo del apartado anterior, pero con una modificación: los triángulos se superponen.
| Nº de triángulos (n) |
1
|
2
|
3
|
4
|
| Nº de cerillas (c) | 3 |
5 |
7 |
9 |
¿Cuál es la fórmula que relaciona el número de cerillas con el número de triángulos?
- El valor numérico de 4a-2b para a=1 y b=0 es .
- El valor numérico de
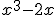 para x = -1 es
.
para x = -1 es
. - El valor numérico de
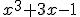 para x = 2 es
.
para x = 2 es
. - El valor numérico de
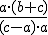 para a = 3, b = 4 y c = 5 es
.
para a = 3, b = 4 y c = 5 es
. - Para que la expresión algebraica 5x+8 valga 3, debe ser x = .