1.2. Simbolización y generalización
Efectivamente, estamos rodeados de símbolos, y algunos son tan comunes que ni siquiera somos conscientes de las ventajas que tienen su uso. Veamos cómo el uso de símbolos es fundamental en matemáticas.
 |
| voluntario, por el conocimiento libreluis de bethencourt, CC by 2.0 de |
Ana colabora en una asociación como voluntaria. Dependiendo del tiempo del que disponga, puede desarrollar su labor en Jornada Completa (8 horas), a Media Jornada (4 horas) o a Horas Sueltas.
Cada día, cuando los voluntarios llegan a la sede de la asociación, anotan el tipo de jornada que van a dedicar en una ficha como ésta:
| Nombre |
Jornada Completa |
Media Jornada |
Horas sueltas |
||||||||||||
| Ana |
x | x |
x |
x |
x |
x | x | ||||||||
Y al final del mes, la asociación genera un resumen de la dedicación de sus voluntarios:
| Nombre |
C | M | S |
| Ana |
4 |
2 |
1 |
| Manuel |
6 |
0 |
2 |
| Javi |
1 | 7 |
6 |
| Marta |
12 |
1 |
0 |
Como ves, C, M y S son letras que equivalen a diferentes números según cada caso. En matemáticas, a estas letras las llamaremos variables. Las variables no sólo nos sirven para organizar información, sino también para trabajar con números de una forma generalizada. Es decir, no necesito saber cuánto vale C para poder hacer determinados cálculos.
Por ejemplo, si a final de mes quiero saber cuántas horas ha dedicado alguien en días a Jornada Completa, tendré que multiplicar el número de días que ha tenido esa jornada (C) por 8, que es el número de horas que se dedican esos días. Es decir: C·8
Cuando trabajamos con números y letras, hay algunas reglas que debemos seguir. Una de ellas es que, si multiplicamos un número por una letra, primero escribiremos el número y luego la variable. En nuestro caso quedaría: 8·C
Otra regla es que, si estamos multiplicando un número por una variable, no es necesario escribir el símbolo del producto. Por lo tanto, el número de horas que dedica alguien mensualmente en Jornadas Completas será 8C
Sabiendo esto ¿serías capaz de escribir con números y las variables C, M y S cuántas horas dedica un voluntario mensualmente?
Lo que hemos obtenido en el ejemplo anterior es una Expresión Algebraica, que es aquélla en la que usamos números y letras relacionadas por operaciones matemáticas, como por ejemplo:
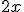 |
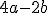 |
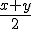 |
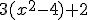 |
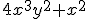 |
Cada expresión algebraica tiene un significado. De hecho, cuando tenemos un problema, intentamos traducirlo al lenguaje algebraico mediante una expresión. Mira los siguientes ejemplos:
|
Enunciado
(lenguaje usual) |
A un número le sumamos 4 unidades |
El doble de un número |
La cuarta parte de un número, menos su cuadrado | El precio de x kg. de naranjas, si valen a 1,80 €/kg. | El 15% de un precio |
|
Expresión algebraica
(lenguaje matemático) |
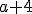 |
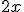 |
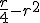 |
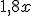 |
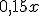 |
Por último, también nos puede servir para buscar generalizaciones de un problema.
Imagina que construimos triángulos con palillos del siguiente modo:
| Nº de triángulos (n) |
1 |
2 |
3 |
4 |
| Nº de palillos (p) | 3 |
6 |
9 |
12 |
¿Podríamos averiguar cuántos palillos necesito si quiero formar 100 triángulos? Para ello tenemos que encontrar una relación entre el número de triángulos (n) y el número de palillos (p). Si te fijas, por cada triángulo necesito 3 palillos, por lo que podríamos deducir que p=3n. Conociendo esta regla, ya puedo saber que para n=100 será p=3·100=300 palillos.
En el siguiente enlace a una página editada por la Junta de Andalucía, tienes actividades que te van a permitir practicar lo dicho en este apartado. Cuando termines una actividad, pulsa el botón superior que dice "LengAlg02", y realiza los tests correspondientes hasta "LengAlg05".