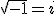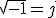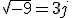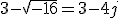Los números complejos se pueden expresar de forma binómica, polar y exponencial; pero a nosotros nos basta con las dos primeras.

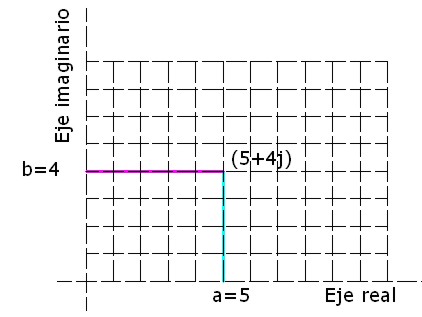
• Forma binómica: la formarán un par de números reales, al primero, a, se le denomina parte real y al segundo, b, parte imaginaria; pudiéndose escribir en la forma (a,b) o (a+bj). Si llevamos al valor de a sobre la abscisa de unos ejes coordenados y b sobre la ordenada, la intersección de las proyecciones me dará un punto, que desde el origen se corresponderá con el módulo de un fasor. A a la llamamos parte real y a b parte imaginaria.

Imagen 12: Complejo en forma binómica. Fuente: Elaboración propia.

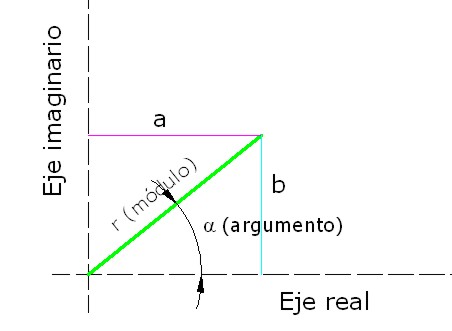
• Forma polar: el mismo punto anterior lo podíamos haber representado si hubiéramos conocido el módulo del fasor y el valor del ángulo que forma con la horizontal o argumento. En este caso lo expresamos de la forma r_α:

Imagen 13: Complejo en forma polar. Fuente: Elaboración propia.

Antes de pasar al último apartado puede ser interesante aclarar por qué a los ejes los llamamos real e imaginario. Para ello pensemos en un número, a, que podemos representar en una recta numérica; este número es un número real.

Imagen 14: Representación de a. Fuente: Elaboración propia.

Si lo multiplicamos por -1, tendremos -a, también número real, con lo que si lo representamos nos quedará:

Imagen 15: Representación de -a. Fuente: Elaboración propia.

Observa que al multiplicar por si mismo el valor de j:

se obtiene (-1) y si te fijas la representación de -a se obtiene al multiplicar a por -1, que en definitiva es como si hubiéramos girado a 180º. Así pues, podemos imaginar que si multiplicamos un número a por √‾-1, es decir, por j, en vez de girarlo 180º lo estaríamos girando 90º; es decir, que un número complejo del tipo a+bj puede representarse llevando a al eje horizontal o real y b al eje vertical o imaginario.