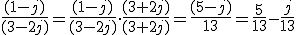3.2. Operaciones con Complejos
Para poder operar con complejos es necesario saber primero que es un complejo conjugado y un opuesto.
Dado el complejo en forma binómica (a+bj), su conjugado será (a-bj); es decir, sus partes reales son iguales y las imaginarias tienen signos opuestos. Si el complejo está en forma polar rα el conjugado será r-α ; es decir, al argumento tiene signo opuesto.
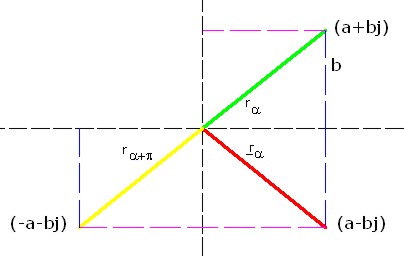
Por otro lado, tendremos complejos opuestos cuando estando en forma binómica, los signos de la parte real e imaginaria sean opuesto, es decir, si tenemos (a+bj), el opuesto será (-a-bj). Otro ejemplo; si tenemos (-a+bj) el opuesto será (a-bj). Si el complejo está en forma polar, el opuesto de rα será rα+π . La imagen inferior tal vez ayude a aclarar estos conceptos. El complejo representado en verde (a+bj) tiene un conjugado en rojo (a-bj) y un opuesto en amarillo (-a-bj); en la imagen también se muestra su notación polar.
 |
|
Imagen 17: Complejos, Conjugados y Opuestos. Fuente: Elaboración propia. |
- Suma de complejos: De manera general, se suman complejos en su forma binómica, dada su sencillez. Se procede sumando por un lado las partes reales y por otro las imaginarias. Por ejemplo:
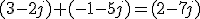 |
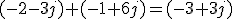 |
| |
- Producto de complejos: Para multiplicar complejos en forma binómica se procede multiplicando todos los términos de uno por todos los del otro, recordando que j·j=√‾-1·√‾-1=-1
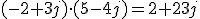 |
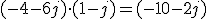 |
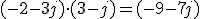 |
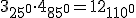 |
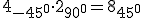 |
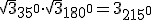 |
- División de complejos: Para dividir complejos en forma binómica tenemos que recurrir a la forma conjugada del complejo denominador, multiplicando numerador y denominador por el mencionado conjugado.
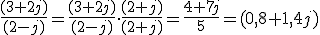 |
Si el complejo viene dado en forma polar, entonces se dividen los módulos y se restan los argumentos.
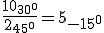 |
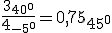 |
Resuelve las siguientes operaciones con complejos:
- (2+j)-(3-2j)
- (-3-2j)·(2-5j)
- 425º·375º
- (-1-j)/(2+2j)
- 525º/240º
- (3+2j)·(-1-5j)