3.1. Cambio de Forma de Complejos
Una vez que conocemos las distintas formas de representar los números complejos, vamos a ver de qué manera se puede pasar de una a otra.
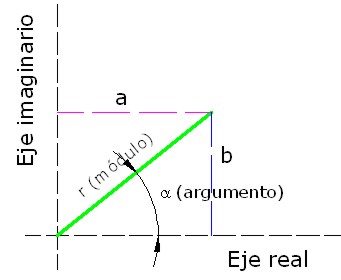
- Paso de forma binómica a polar: Tal y como indica la gráfica inferior el complejo en forma binómica será a+bj;
 |
|
Imagen 16: Representación de un Número Complejo.
Fuente: Elaboración propia. |
por lo que para obtener el módulo del fasor, r, habrá que aplicar Pitágoras en el triángulo rectángulo formado por a, b y r:
 |
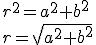Si queremos obtener el ángulo alfa, α, recurriremos a la razón trigonométrica tangente:
 |
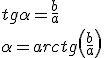- Paso de forma polar a binómica: En este caso, tendremos el complejo expresado en la forma rα y no es que lo anterior haya sido difícil, pero este paso es aún más sencillo. Basta con aplicar las relaciones trigonométricas seno y coseno.
 |
 |
Ejemplo o ejercicio resuelto
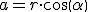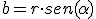Vamos a practicar lo expuesto anteriormente con unos ejemplos. Dado su sencillez, solo se indican los resultados de cada ejercicio.
Pasa de forma los siguientes complejos:
-
A forma polar
- (3-2j)
- (-5+2j)
- (-2-5j)
-
A forma binómica
- 4,525º
- 1275º
- 8225º
Objetivos
Puede ser interesante que te pongas tú unos cuantos ejemplos y que practiques. La mayoría de las calculadoras convierten complejos, así que busca el manual y lo refrescas que así sacarás partido a esa máquina que te costó tan cara y solo usas para cuatro cosas. Si ese no fuera tu caso, tal vez te venga bien visitar esta página de números complejos.
Por si tu navegador te da problemas, aquí te dejo la dirección para que la uses con el que prefieras: