3.2. Intersecciones
Determinar la recta intersección de un plano con el segundo plano bisector.
En el apartado 2.1 determinamos la intersección de una recta horizontal y frontal con el segundo plano bisector (segundo y cuarto cuadrante respectivamente).
Para poder determinar la intersección de un plano con el segundo plano bisector solamente tenemos que obtener los puntos de contacto de dos de sus rectas con dicho plano. Para simplificar el proceso y el trazado generalmente se usan rectas notables, como en el apartado 2.1.
En la animación inferior puedes ver cómo se ha obtenido la recta M intersección entre el plano dado P y el segundo plano bisector, para ello hemos empleado dos rectas notables de dicho plano oblicuo:
- Horizontal R = punto A.
- Frontal S = punto B.
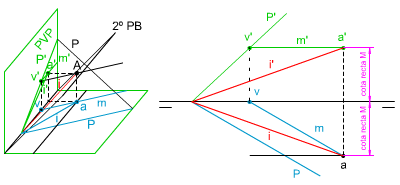 |
En la imagen izquierda puedes ver cómo se ha determinado la recta intersección de un plano oblicuo con el primer plano bisector.
Te pedimos que dibujes las proyecciones de dicha recta intersección I. |