3.1. Recta y plano
En la siguiente animación puedes ver los cuadrantes por los que pasa el plano P, y el espacio que ocupa en cada uno de ellos.
Trazas de un plano determinado por dos de sus rectas paralelas.
Como ya vimos en el curso pasado, un plano queda definido por tres puntos no alineados, dos rectas que se cortan o son paralelas, y un punto y una recta; así pues, para poder determinar los cuadrantes por los que pasa un plano es necesario obtener sus trazas, esto es, los puntos trazas de dos rectas que pertenezcan a dicho plano.
En la siguiente animación te mostramos cómo se han determinado las trazas de un plano oblicuo que pasa por los cuatro cuadrantes, dadas dos de sus rectas paralelas.
Observa que dichas trazas se obtienen al unir las trazas homónimas de ambas rectas (v1' con v2', y h1 con h2).
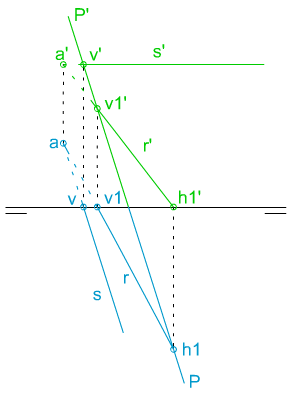 |
En la imagen izquierda puedes ver cómo se han determinado las trazas de un plano dadas las proyecciones de dos rectas que pertenecen a él.
¿Qué tipo de plano se ha obtenido? |