3.3. Perpsectiva Cónica
| HOMOLOGÍA | PERSPECTIVA CÓNICA |
| Recta Límte |
Línea del horizonte |
| Eje | Línea de Tierra |
| Centro |
Punto de Vista |
| Origen | Perspectiva |
| Transformada | Figura abatida |
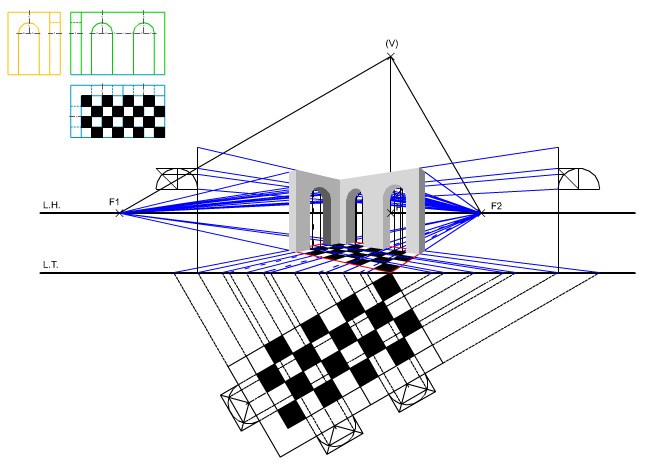
Para que puedas relacionar dicho elementos en la siguiente animación te mostramos cómo se dibuja la perspectiva cónica oblicua de un cuadrilátero.
Observa detenidamente el trazado y la correspondencia entre los siguientes elementos: (V), LH, LT, F1, F2.
Perspectiva cónica frontal.
En el apartado 2.3 te mostramos cómo se transformaba una circunferencia en una elipse, ahora vas a ver, en la animación inferior, el mismo trazado mediante perspectiva cónica.Para ello hemos inscrito dicha circunferencia en un cuadrado cuyos lados son paralelos y perpendiculares a la LT (perspectiva frontal), realizando la perspectiva de dicho paralelogramo podemos obtener la curva cónica.
Perspectiva cónica oblicua.
Este caso es similar al anterior, salvo la disposición del cuadrado cuyos lados son oblicuos al eje (perspectiva oblicua).
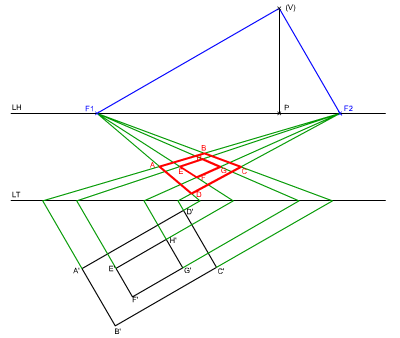 |
En la figura de la izquierda puedes ver cómo se ha realizado la perspectiva cónica oblicua de dos paralelogramos rectángulos, observa que dicha representación es una transformación homológica de un cuadrilátero. Te pedimos que dibujes dicha perspectiva-transformación. Para resolverlo debes repasar los conceptos y procedimientos explicados en las animaciones anteriores de este apartado y de los anteriores. Material necesario:
|