3.1. Transformaciones
Actividad
El problema consiste en determinar el centro de homología de manera que este satisfaga unas condiciones prestablecidas.
Transformar un triángulo escaleno dado ABC en otro equilátero.
El centro de homología debe estar en la intersección de dos arcos capaz de ángulo 60º.
En la animación inferior te mostramos el procedimiento que debes seguir para dibujar dicho triángulo homólogo.
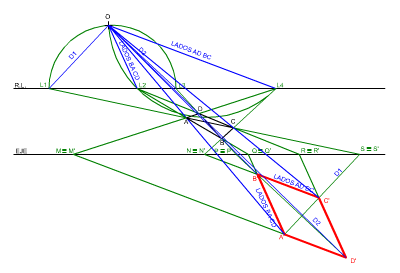
Transformar un cuadrilátero dado ABCD en un paralelogramo cuadrado.
Para transformar un cuadrilátero en un paralelogramo, dos pares de lados del primero (figura origen) deben converger en un punto de la recta límite, así se consigue que sus homólogos sean paralelos (condición necesaria).
La disposición del centro de homología dependerá del tipo de paralelogramo que se quiera obtener.
En la siguiente animación puedes ver cómo se ha trazado un paralelogramo rectángulo A'B'C'D' homólogo a un cuadrilátero dado ABCD, el centro de homología se ha determinado según los siguientes parámetros: la perpendicularidad de sus lados y el ángulo que forman las diagonales.
Pre-conocimiento
Caso de estudio
 |
En la figura de la izquierda te mostramos cómo se ha convertido el cuadrilátero dado ABCD en un rombo mediante homología (ángulo Bº = Dº = 45º). Te pedimos que dibujes dicha transformación. Para resolverlo debes repasar los métodos explicados en las animaciones anteriores. Material necesario:
|