1.3. Entramos en quirófano
 |
| Imagen de Chesi bajo licencia Creative Commons |
Actividad
|
| Imagen de Carlos Urzua bajo licencia Creative Commons |
Recuerda que dos sucesos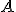 
y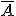 
son contrarios cuando al realizar una experiencia aleatoria:
- Son incompatibles.
- Se obtiene siempre uno de los dos.
El suceso seguro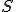 
y el suceso imposible 
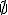son un ejemplo de sucesos contrarios.
Ejemplo:
Experimento aleatorio: Lanzamiento de un dado.
Sucesos:
A="Obtener un número impar".
B="Obtener un número par".
A y B son incompatibles, pero siempre se da uno de los dos. A y B son sucesos contrarios.
Si los sucesos son:
A="Obtener un número mayor que 0".
B="Obtener un número menor que 0", el segundo no puede darse nunca, mientras que el primero se da siempre.
Ejemplo o ejercicio resuelto
|
| Imagen de Gato Azul bajo licencia Creative Commons |
Después de la partida de bingo de nuestros amigos, empezó una de dados, donde se apostaban quién pagaba la cena.
El experimento consistía en lanzar un dado y anotar el resultado, y los sucesos eran los siguientes:
A="Salir un número impar" (ganaba Gonzalo).
B="Salir un número primo" (ganaba Blanca).
C="Salir un divisor de 6"(ganaba M.ª José).
D="Salir un múltiplo de 4" (ganaba la amiga de M.ª José).
a) ¿Cuáles son los elementos del suceso donde ganan Gonzalo o Blanca?
b) ¿Cuáles son los elementos del suceso donde ganan M.ª José o su amiga?
c) ¿Cuáles son los elementos del suceso donde ganan Gonzalo y Blanca?
d) ¿Cuáles son los elementos del suceso donde ganan M.ª José y su amiga?
e) ¿Cuáles son los elementos del suceso donde gana Gonzalo y no gana Blanca?
f) ¿Cuáles son los elementos del suceso donde gana Blanca y no gana M.ª José?
.
.
.
.
.
.
.
AV - Reflexión
En la página del proyecto ed@d (Enseñanza Digital a Distancia), tienes varias actividades donde puedes practicar con las operaciones entre sucesos. Haz clic en la siguiente imagen y elige la opción de "Espacio muestral y sucesos".
Actividad
Llamamos suceso unión de A y B al que se produce cuando se realiza A o B. Se representa por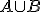 
.
Llamamos suceso intersección de A y B al que se produce cuando se realizan simultáneamente los sucesos A y B. Se representa por 
.
Llamamos suceso diferencia de A y B al que se produce cuando se realiza el suceso A pero no se realiza el B. Se representa por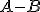 
.
Existen dos leyes que son muy útiles a la hora de operar con sucesos contrarios; las leyes de De Morgan:
1.- El suceso contrario de la unión de dos sucesos es la intersección de sus sucesos contrarios:.
2.- El suceso contrario de la intersección de dos sucesos es la unión de sus sucesos contrarios:.
Ejemplo o ejercicio resuelto
Comprueba que se cumplen las leyes de Morgan con los sucesos de la partida de dados de nuestros amigos.
Comprueba que se cumplen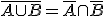 
y 
.
, 
, 
, 
, 
Pre-conocimiento
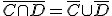Aquí tienes un vídeo para que practiques en el lanzamiento de dados.
Augustus De Morgan
 |
| Imagen de Wikimedia Commons |
De Morgan fue tutor de Lady Ada Lovelace, amiga de su esposa Sofía e hija de Lord Bayron.
Se cuenta que Babbage, Ada y De Morgan formaron una sociedad de apuestas en las carreras de caballos convencidos de que sus conocimientos sobre probabilidad les servirían para ganar el suficiente dinero para financiar la máquina para calcular que había diseñado Babbage. Al poco tiempo se convencieron de que no podían controlar con la probabilidad los caballos que iban a ganar.
Escribió libros sobre varios temas, aritmética, álgebra, análisis, lógica, siendo esta última el campo en el que más sobresalió.
Una de sus grandes aportaciones, son las leyes que llevan su nombre y que acabamos de ver en este tema.
De Morgan también estuvo interesado en la historia de las matemáticas y era un apasionado, como el que os escribe, de los acertijos matemáticos, llegando incluso a escribir algún libro sobre el tema.
En uno de sus acertijos decía De Morgan que él tenía x años en el año x2.
¿Serías capaz de averiguar cuántos años tenía y en qué año, sabiendo que nació en 1806 y murió en 1871?
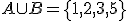
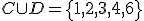
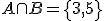
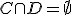
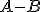
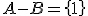
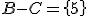
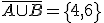
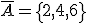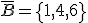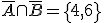
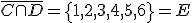
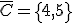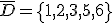