1.2. Las comparaciones son odiosas
Si tenemos una función 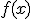 llamamos derivada de la función en un punto
llamamos derivada de la función en un punto 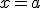 a la tasa de variación instantánea de la función en el punto
a la tasa de variación instantánea de la función en el punto  y se denota
y se denota 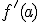 . Así, según la definición tenemos que:
. Así, según la definición tenemos que:
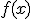 llamamos derivada de la función en un punto
llamamos derivada de la función en un punto 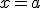 a la tasa de variación instantánea de la función en el punto
a la tasa de variación instantánea de la función en el punto  y se denota
y se denota 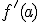 . Así, según la definición tenemos que:
. Así, según la definición tenemos que:
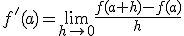
Recuerda que para que exista este límite, deben existir los límites laterales y coincidir. Así, de la misma forma, podemos definir las derivadas laterales como:
.- Derivada por la derecha:
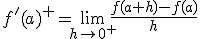
.- Derivada por la izquierda:
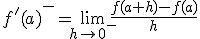
Geométricamente, la derivada de una función en un punto es la pendiente de la recta tangente a la gráfica de la función en dicho punto.
Podemos comprobar en la escena de GeoGebra del apartado anterior, cómo efectivamente si hacemos coincidir a y b, la recta secante se convertirá en la recta tangente.
Halla la pendiente de la recta tangente a la gráfica de
en el punto de abscisa x=-2.
Completa en la siguiente tabla las derivadas en los puntos de abscisas -2, -1, 0, 1, 2, 3 y 4 de la función f(x)=x2-2x.
| x | -2 | -1 |
0 |
1 |
2 |
3 |
4 |
| f'(x) |
|
Si una función es derivable en un punto x = a, entonces es continua para x = a.
El reciproco es falso, es decir, hay funciones que son continuas en un punto y que, sin embargo, no son derivables.
Observa, la siguiente animación de GeoGebra. En ella puedes hacerte una idea intuitiva y gráfica de lo que es una función continua pero no derivable. Está relacionado con la "suavidad" de sus curvas.
Por cierto, efectivamente f(x)=|x| es continua en x=0 pero no derivable.
Estudiar la continuidad y derivabilidad de la función f(x)=|x-1|
En este enlace a la página vitutor, puedes encontrar algunos ejercicios resueltos sobre la relación existente entre continuidad y derivabilidad.
