2.3. Derívame
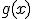 y
y 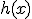 , la derivada de la suma y el producto de ambas se obtiene de la siguiente forma:
, la derivada de la suma y el producto de ambas se obtiene de la siguiente forma:
|
|
|
|
Derivada de la suma de funciones
|
Derivada del producto de funciones
f'(x)=g'(x)h(x)+h'(x)g(x) |
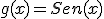 y
y 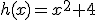 Calcula la derivada de la suma y el producto de ambas.
Calcula la derivada de la suma y el producto de ambas.
|
|
Normalmente, las funciones que solemos encontrarnos no son funciones simples como las que vemos en la tabla de derivadas, sino que son funciones que se obtienen como composición de funciones simples.
Por ejemplo 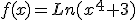 , en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.
, en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.
Si llamamos 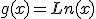 y
y 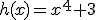 tenemos que
tenemos que 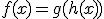 .
.
la regla de la cadena nos dice que
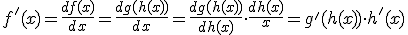
En nuestro caso 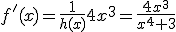
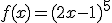
Una aplicación de la regla de la cadena para las funciones trigonométricas la observamos en el siguiente vídeo:
|
|
En la ventana interactiva, a la que accedes desde el siguiente enlace, vas a poder practicar realizando distintas derivadas según los modelos que se proponen. Elige una opción y comprueba que la fórmula que sale es la que corresponde. Seguidamente realiza la derivada que te proponen y comprueba que la has hecho bien. Cada vez que pulses sobre el botón "Otro ejercicio" aparecerá un nuevo ejercicio sobre ese modelo de derivada. ¿Te van saliendo todas?
Ahora te toca practicar a tí. Para ello te proponemos que calcules la derivada de cada una de las siguientes funciones:
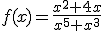
Escribe la función, pulsa "Apply", selecciona la
variable respecto a la que quieres derivar y después
"Compute" tantas veces como sea necesario para calcular la derivada
final. Esta calculadora va aplicando la regla de la cadena. |
|
Calculadora de derivadas obtenida de la página de José María Gómez Aroca |
Si ahora tenemos una función 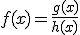 te proponemos que, aplicando todo lo anterior, calcules su derivada.
te proponemos que, aplicando todo lo anterior, calcules su derivada.
En el siguiente cuadro puedes observar un resumen de casi todo lo tratado a lo largo del tema. Pulsa sobre los botones que aparecen que te guiarán por el resumen:
|
|
| Animación realizada por Salvador Hurtado |
Para que te sea más práctico, ponemos a tu disposición dos tablas de derivadas que recogen todo lo anterior, para que utilices la que te resulte más cómoda: tabla 1, tabla 2.
Ahora te toca practicar todo lo que puedas los contenidos de la unidad. Para seguir profundizando en la práctica con derivadas te facilitamos este documento:
Además, puedes seguir practicando los contenidos en esta web.
Te ofrecemos además otra calculadora de derivadas.
También puedes observar la siguiente calculadora de derivadas que las realiza paso a paso utilizando la regla de la cadena.
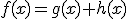
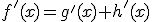
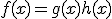
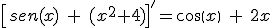 .
.
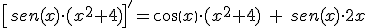 .
.
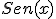 se escribe sin(x), y que
se escribe sin(x), y que 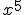 se escribe x^5
se escribe x^5
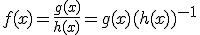
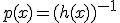
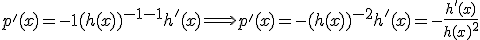
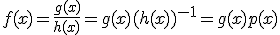
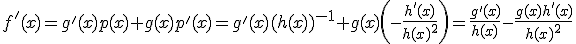
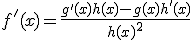 Este es un resultado importante que deberás utilizar a la hora de calcular la derivada de un cociente.
Este es un resultado importante que deberás utilizar a la hora de calcular la derivada de un cociente.