4.3. Nos complementamos
Si tenemos una función diremos que es logarítmica si tiene la forma 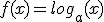 donde
donde 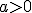 es un número.
es un número.
Entre sus propiedades podemos citar que:
|
|
| Función logarítmica. Animación obtenida del banco de imágenes del ITE. |
1.- El dominio son todos los valores que sean mayores que cero. Por tanto, no se corta con el eje de ordenadas
2.- No es par ni impar.
3.- Si 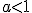 es una función decreciente y si
es una función decreciente y si 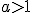 es una función creciente.
es una función creciente.
4.- Se corta con el eje de abcisas en el punto 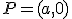 .
.
Practica en la siguiente ventana con distintos valores de  y comprueba que todas las propiedades anteriores son ciertas.
y comprueba que todas las propiedades anteriores son ciertas.
 |
| Tensiómetro. Imagen obtenida del banco de imágenes del ITE. |
En una revisión rutinaria de un hospital, la empresa de matenimiento ha detectado que uno de los tensiómetros del quirófano necesita un ajuste ya que los valores que aparecen en la pantalla no son correctos. Según han calculado deben aplicar la siguiente corrección:
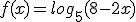 donde
donde 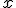 son los valores que aparecen actualmente en la pantalla.
son los valores que aparecen actualmente en la pantalla.
Calcula los valores a los que se les podrá aplicar esta corrección:
Un función diremos que es exponencial si tiene la forma 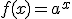 con
con 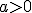 .
.
Observa el siguiente vídeo:
|
|
Imagina que estás calculando las potencias de 2: 2, 4, 8, 16, 32, 64, .... Esos valores se pueden obtener de la función 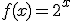 dándole como valores de x los números naturales.
dándole como valores de x los números naturales.
|
|
| Función exponencial. Imagen obtenida del Banco de Imágenes del ITE. |
En la siguiente ventana puedes dibujar cualquier función exponencial. Utilízala para indicar cuáles de las siguientes afirmaciones son verdaderas.
Verdadero Falso
Verdadero Falso
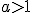 la función es creciente.
la función es creciente.
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
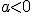 la función es impar.
la función es impar.
Verdadero Falso
Utiliza la ventana interactiva que aparece más abajo para representar gráficamente las siguientes funciones. reflexiona sobre la imagen obtenida:
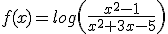
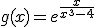
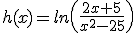
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
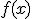 y eso lo puedes ver en el siguiente vídeo.
y eso lo puedes ver en el siguiente vídeo.