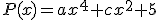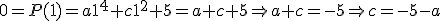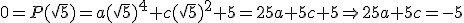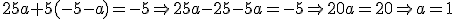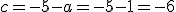5. Especial selectividad
|
|
Sea 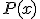 una función polinómica de grado 4 de la que sabemos que su gráfica es simétrica y que cumple que
una función polinómica de grado 4 de la que sabemos que su gráfica es simétrica y que cumple que 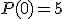 . Si dos de sus raices son
. Si dos de sus raices son 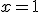 y
y 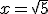 . determina la función.
. determina la función.
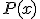 una función polinómica de grado 4 de la que sabemos que su gráfica es simétrica y que cumple que
una función polinómica de grado 4 de la que sabemos que su gráfica es simétrica y que cumple que 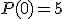 . Si dos de sus raices son
. Si dos de sus raices son 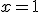 y
y 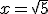 . determina la función.
. determina la función.
Se considera la función
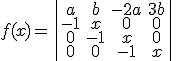
Determina  y
y 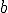 sabiendo que
sabiendo que 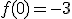 y que
y que 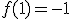
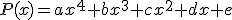 Como sabemos que su gráfica es simétrica, tenemos que los coeficientes correspondientes a los grados impares son nulos, por lo que
Como sabemos que su gráfica es simétrica, tenemos que los coeficientes correspondientes a los grados impares son nulos, por lo que 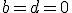 .
.
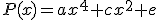 . Además, como
. Además, como 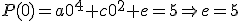 Por tanto:
Por tanto: