1.3. Uno de cada
En este apartado vamos a comenzar contándote un chiste. Un chiste matemático que puedes encontrar con facilidad en Internet.
 |
Le preguntan a un matemático: "Tú que harías si te encontrarás una casa ardiendo y justo enfrente una manguera sin conectar junto a una boca de riego". El matemático responde: "Obviamente conectaría la manguera y comenzaría a lanzar agua a la casa". "Bueno, ¿y si la manguera estuviera conectada pero la casa no estuviera ardiendo?". A lo que responde de nuevo el matemático: "Desconectaría la manguera, prendería fuego a la casa y después aplicaría el método anterior".
Quizás el chiste no te haya hecho mucha gracia, sobretodo si eres bombero, pero refleja bien un método de resolución que se utiliza en ciencia y, especialmente, en matemáticas. Cuando estamos resolviendo un problema y llegamos a una situación que ya sabemos resolver se puede considerar que el problema está resuelto. Por eso dentro de los procedimientos de resolución de problemas tenemos el dividir un problema en partes o el buscar un problema similar que sepamos resolver.
Esto nos va a servir para este último apartado del punto 1 pues lo que vamos a hacer es reducir el problema a cosas que ya hemos visto en los apartados anteriores.
Importante
Para hallar la distancia entre una recta y un plano debemos prestar atención, como en los apartados anteriores, a las posiciones relativas que tengan dichos elementos.
 |
Si la recta corta al plano o está incluida en él, directamente la distancia entre ambos es cero.
Si la recta es paralela al plano, todos los puntos de la recta se encuentran a la misma distancia del plano. Por tanto, basta tomar un punto cualquiera de la recta y hallar la distancia al plano como vimos en el apartado anterior.
Ten cuidado porque no es lo mismo elegir un punto del plano y hallar la distancia a la recta, pues ese punto puede no estar sobre la perpendicular.
AV - Actividad de Espacios en Blanco
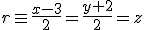y el plano 
.
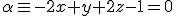Escribe si o no en los siguientes cuadros, según corresponda.
- La recta corta al plano.
- La recta es paralela al plano.
- La recta está contenida en el plano.
La distancia entre la recta y el plano es de unidades.
Para saber más
En la siguiente dirección de Internet tienes una serie de applet que te calculan directamente las distancias entre rectas y planos y te repasan los conceptos que hemos visto en este primer apartado.
Una vez que hayas resuelto cualquier actividad, puedes comprobar si lo que has obtenido es correcto o no antes de pasar a otra cosa.