1.1. De recta a recta
 |
Si pudiéramos tener las ecuaciones que correspondieran a esos elementos en un sistema de referencia tridimensional entonces bastaría echar mano de unas pocas fórmulas para encontrar de una forma precisa cuál es esa distancia. Eso es lo que vamos a intentar en este apartado.
Antes de hallar la distancia entre dos rectas vamos a ver como hallar la distancia desde un punto cualquiera a una recta, puesto que ese proceso lo necesitaremos posteriormente. Además, es muy parecido a lo que vamos a hacer en el resto de los casos.
La distancia de un punto P a una recta r es la medida desde el punto P al pie de la perpendicular que corta a la recta y que pasa por P.
El modo más fácil de hallarla es elegir un punto Q genérico de la recta r e imponer que el vector 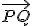 sea perpendicular a la recta , es decir, a su vector de dirección. De esa forma calculamos el punto Q que está en la perpendicular y basta hallar la distancia entre los puntos P y Q.
sea perpendicular a la recta , es decir, a su vector de dirección. De esa forma calculamos el punto Q que está en la perpendicular y basta hallar la distancia entre los puntos P y Q.
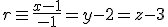
Hay otros métodos para hallar la distancia de un punto P a una recta r.
- Podemos hallar el plano que pasa por P y es perpendicular a r. Es muy fácil pues de ese plano conocemos un punto por donde pasa (P) y su vector dirección que sería el vector normal al plano. Una vez que tenemos el plano, basta hallar el punto de corte con la recta y obtenemos el punto Q. La distancia del punto a la recta es el módulo del vector
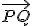 .
. - Como vimos en el tema anterior, si tenemos dos vectores independientes el módulo del producto vectorial es el área del paralelogramo construido sobre ellos. Otro método sería elegir un punto A cualquiera de r y hallar el área del paralelogramo construido sobre los vectores
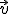 y
y 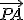 . La distancia del punto P a la recta r es la altura de ese paralelogramo. En el punto 2 veremos otro método que permite hallar la distancia y la recta que corta perpendicularmente a las dos rectas con los mismos cálculos.
. La distancia del punto P a la recta r es la altura de ese paralelogramo. En el punto 2 veremos otro método que permite hallar la distancia y la recta que corta perpendicularmente a las dos rectas con los mismos cálculos.
El método para rectas que se cruzan puedes verlo en el applet siguiente en el que puedes introducir las coordenadas del punto y de la recta. Solo tienes que cambiar en Paso nº para ver como se construye.
Applet de Descartes creado por Juan Simón Santamaría bajo licencia Creative Commons.
 |
| Imagen Rio Po (vista aerea) de Alessandro Quisi tomada del Banco de Imágenes del ITE |
Para calcularla se ha sacado una foto de la comarca desde un satélite y se han asignado valores a esos elementos. El complejo está situado, según la distribución asignada, en el punto 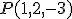 y la línea del rií, que es bastante recto en esa zona, tendría de ecuación
y la línea del rií, que es bastante recto en esa zona, tendría de ecuación 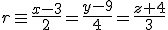 .
.
La distancia sobre dos rectas se define como la menor distancia que hay entre dos cualesquiera de sus puntos. Su distancia depende, por tanto, de la posición relativa que tengan esas dos rectas. Tenemos los siguientes casos:
- Si las rectas se cortan o son coincidentes su distancia es cero, ya que hay al menos un punto común a las dos rectas y la distancia de un punto a sí mismo es nula.
- Si las dos rectas son paralelas, basta tomar un punto cualquiera de una de ellas y hallar la distancia a la otra recta como hemos visto antes. Ojo, no es lo mismo elegir un punto cualquiera en cada una de las rectas ya que esos dos puntos no tienen por qué estar sobre la perpendicular.
- En el caso de que las dos rectas se crucen ya se complica un poco. Una forma es tomar un punto de cada recta y con el vector formado por esos dos puntos y los dos vectores de dirección formamos un paralelepípedo cuyo volumen sabemos calcular del tema anterior. Como el volumen es igual al producto de la base (que es un paralelogramo y también sabemos calcularla) por la altura, que es precisamente la distancia buscada, podemos despejar la altura y tenemos la distancia. En el siguiente applet puedes ver los pasos que se siguen para resolverlo.
Applet de Descartes realizado por Juan Simón Santamaría bajo licencia Creative Commons.
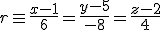 y
y 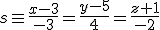 comprueba que son paralelas y halla la distancia entre ellas.
comprueba que son paralelas y halla la distancia entre ellas.
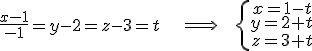
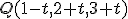
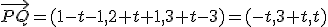 e imponemos que sea perpendicular al vector dirección de r
e imponemos que sea perpendicular al vector dirección de r 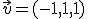 .
.
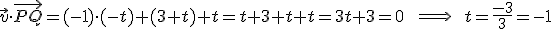
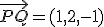 y la distancia pedida sería
y la distancia pedida sería
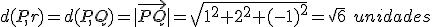
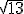 u.
u.