3.2. Sistemas con parámetros
Aunque no hemos visto este tipo de ejercicio dentro de los contenidos, suelen ser lo más corriente dentro de los exámenes de Selectividad. Consiste en estudiar como sería un sistema en el que uno o más de los coeficientes están sustituidos por un parámetro. Según el valor que se le dé a ese parámetro, el sistema será de distinto tipo. Ejercicios parecidos has visto en el tema anterior cuando te pedían calcular el rango o la matriz inversa dependiendo de un valor no conocido.
Sea el sistema de ecuaciones 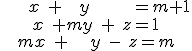
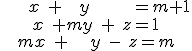
a) Determina los valores de m para los que el sistema es compatible.
b) Resuelve el sistema en el caso m=-1.
Considera el sistema de ecuaciones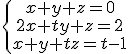
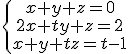
a) Determina el valor de t para que el sistema sea incompatible.
b) Resuelve el sistema para t=1.
Dado el siguiente sistema de ecuaciones 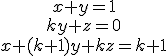
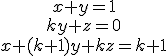
a) Determina el valor del parámetro k para que el sistema sea incompatible.
b) Halla el valor del parámetro k para que la solución del sistema tenga z=2.
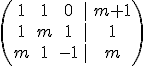 . Ahora estudiamos el rango de la matriz de los coeficientes. Para ello tenemos en cuenta que ya hay un menor de orden 2 distinto de cero
. Ahora estudiamos el rango de la matriz de los coeficientes. Para ello tenemos en cuenta que ya hay un menor de orden 2 distinto de cero 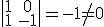 . Este paso incluso nos lo podíamos haber ahorrado englobándolo en el siguiente.
. Este paso incluso nos lo podíamos haber ahorrado englobándolo en el siguiente.
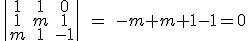 y vemos que, independientemente del valor de m, la matriz de los coeficientes siempre tiene de rango 2.
y vemos que, independientemente del valor de m, la matriz de los coeficientes siempre tiene de rango 2.
 . Si igualamos a cero, ese determinante se anulará cuando -m²-m=0, es decir, cuando -m(m+1)=0 que es lo mismo que decir que cuando m=0 ó m=-1. Por lo tanto, si m fuese distinto de 0 y de -1, el rango de la matriz ampliada sería 3 y el sistema sería incompatible, y sólo será compatible si m=0 ó m=-1.
. Si igualamos a cero, ese determinante se anulará cuando -m²-m=0, es decir, cuando -m(m+1)=0 que es lo mismo que decir que cuando m=0 ó m=-1. Por lo tanto, si m fuese distinto de 0 y de -1, el rango de la matriz ampliada sería 3 y el sistema sería incompatible, y sólo será compatible si m=0 ó m=-1.
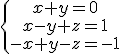 que ya sabemos que es compatible indeterminado. En concreto podemos ver que la tercera ecuación es la misma que la segunda cambiada de signo.
que ya sabemos que es compatible indeterminado. En concreto podemos ver que la tercera ecuación es la misma que la segunda cambiada de signo.
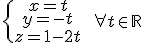 , donde el último símbolo raro significa para todo, es decir, nos dice que para cualquier valor que sustituyamos en t nos da una solución del sistema.
, donde el último símbolo raro significa para todo, es decir, nos dice que para cualquier valor que sustituyamos en t nos da una solución del sistema.
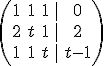 ahora realizamos las siguientes transformaciones:
ahora realizamos las siguientes transformaciones:
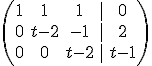 .
.
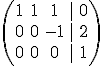 que equivale a un sistema incompatible.
que equivale a un sistema incompatible.
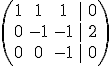 basta reconstruir el sistema
basta reconstruir el sistema 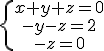 y resolviendo de abajo hacia arriba sale la solución z=0 ; y=-2 ; x=2.
y resolviendo de abajo hacia arriba sale la solución z=0 ; y=-2 ; x=2.
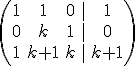 pasamos a
pasamos a 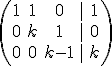 restándole a la tercera fila las dos primeras.
restándole a la tercera fila las dos primeras.
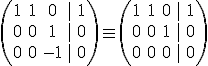 . En este caso el sistema es compatible indeterminado.
. En este caso el sistema es compatible indeterminado.
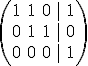 y en este caso es cuando el sistema es incompatible.
y en este caso es cuando el sistema es incompatible.
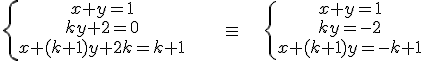
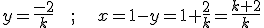 .
.
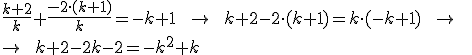
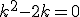 que se cumple para k=0 (imposible pues no tendría sentido el haber dividido por k) y para k=2. Por lo tanto la solución del sistema sería, tomando k=2: x=2; y=-1; z=2.
que se cumple para k=0 (imposible pues no tendría sentido el haber dividido por k) y para k=2. Por lo tanto la solución del sistema sería, tomando k=2: x=2; y=-1; z=2.
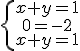 y vemos que la segunda ecuación no tiene sentido.
y vemos que la segunda ecuación no tiene sentido.