3.1. Sistemas con enunciado
Para acabar el tema vamos a ver, como en los temas anteriores, una serie de ejercicios que han aparecido en exámenes de Selectivdad de cursos pasados. Recuerda que este apartado es un complemento y que no es objetivo de estos contenidos el preparar para esa prueba, pero si ayudarte si deseas presentarte a ella.
Una empresa cinematográfica dispone de tres salas: A, B y C. Los precios de entrada a estas salas son 3, 4 y 5 euros, respectivamente. Un día la recaudación conjunta de las tres salas fue de 720 euros y el número total de espectadores fue de 200. Si los espectadores de la sala A hubieran asistido a la sala B y los de la sala B a la sala A, se hubiese obtenido una recaudación de 20 euros más. Calcula el número de espectadores que acudió a cada una de las salas.
Tomamos como variables:
x= nº de espectadores de la sala A
y= nº de espectadores de la sala B
z= nº de espectadores de la sala C
Completa el sistema según los datos reflejados:
x + y + z = 720
x + y + z =
x + y + 5z =
La solución de ese sistema sería
x = espectadores en la sala A
y = espectadores en la sala B
z = espectadores en la sala C
Tratamos de adivinar, mediante ciertas pistas, los precios de tres productos A, B y C.
Pista 1: Si compramos una unidad de A, dos de B y una de C gastamos 390 euros.
Pista 2: Si compramos n unidades de A, n+3 de B y tres de C gastamos 390 euros.
a) ¿Hay algún valor de n para el que estas dos pistas sean incompatibles?
b) Sabiendo que n=4 y que el producto C cuesta el triple que el producto A, calcula el precio de cada producto.
Un cajero automático contiene sólo billetes de 10, 20 y 50 euros. En total hay 130 billetes con un importe de 3000 euros.
a) ¿Es posible que en el cajero haya el triple número de billetes de 10 que de 50?
b) Suponiendo que el número de billetes de 10 es el doble que el número de billetes de 50, calcula cuántos billetes hay de cada tipo.
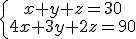 .
.
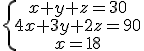 , pero al resolverlo nos saldría como solución x=z=18 e y=-6 y lógicamente es imposible que una moneda pese -6 gramos. Luego la hipótesis de que la sortija pesara 18 gramos no es válida.
, pero al resolverlo nos saldría como solución x=z=18 e y=-6 y lógicamente es imposible que una moneda pese -6 gramos. Luego la hipótesis de que la sortija pesara 18 gramos no es válida.
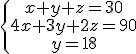 , en cuyo caso la solución sería x=z=6 gramos e y=18 gramos, que si es una solución aceptable.
, en cuyo caso la solución sería x=z=6 gramos e y=18 gramos, que si es una solución aceptable.
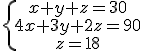 .
.
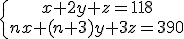 , vamos a utilizar Gauss para estudiarlo.
, vamos a utilizar Gauss para estudiarlo.
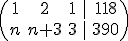 le restamos a la segunda fila la primera multiplicada por n y obtenemos:
le restamos a la segunda fila la primera multiplicada por n y obtenemos: 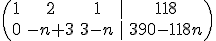 . Vemos que si n=3 entonces
. Vemos que si n=3 entonces 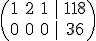 con lo que tenemos un sistema incompatible.
con lo que tenemos un sistema incompatible.
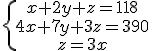 , basta resolverlo y obtenemos los valores A = 69 euros, B = 13 euros y C = 23 euros.
, basta resolverlo y obtenemos los valores A = 69 euros, B = 13 euros y C = 23 euros.
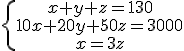 si lo estudiamos es un sistema incompatible, luego no es posible la condición que nos indican.
si lo estudiamos es un sistema incompatible, luego no es posible la condición que nos indican.
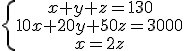 en cuyo caso la solución sería 80 billetes de 10 €, 10 billetes de 20 euros y 40 billetes de 50 €.
en cuyo caso la solución sería 80 billetes de 10 €, 10 billetes de 20 euros y 40 billetes de 50 €.