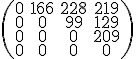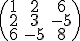1.2. En la variedad está la diversión
 |
Quizás recuerdes que el curso pasado trabajamos con los vectores. Un vector era un conjunto de dos elementos 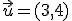 . Si te fijas podemos considerar que ese vector (3 4) es un caso particular de matriz en la que solo hay una fila. En este apartado lo que vamos a ver es distintos tipos de matrices que tienen un nombre particular.
. Si te fijas podemos considerar que ese vector (3 4) es un caso particular de matriz en la que solo hay una fila. En este apartado lo que vamos a ver es distintos tipos de matrices que tienen un nombre particular.
En la siguiente ventana de Descartes puedes ver las definiciones, con ejemplos, de diversos tipos de matrices. Basta que vayas seleccionando cada tipo en la ventanilla superior derecha. Repásalas detenidamente y después realiza las actividades que te planteamos.
Applet de Descartes creado por Alfredo Pena Iglesias bajo licencia Creative Commons.
En el siguiente enlace tienes una serie de preguntas de tipo test donde repasas lo que hemos visto hasta el momento. Hay dos preguntas, la 7 y la 10, que corresponden a elementos que veremos en el apartado 2.4.
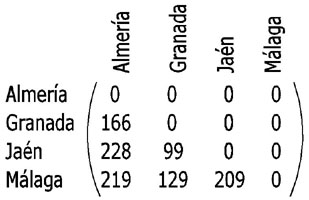 |
En muchos mapas de carreteras aparece la información sobre las distancias entre las capitales de provincias o de países. A partir de esa información podemos construir una matriz de distancias como la siguiente, en la que, para no repetir datos, sólo se escribe la distancia de una ciudad a otra, no de la otra a la una, nos explicamos, si escribimos la distancia de Barcelona a Madrid, no se escribe también la de Madrid a Barcelona, sino que se escribe 0.
En la imagen adjunta tienes la matriz de distancias que hemos construido con los kilómetros que hay entre las capitales de Andalucía Oriental. A partir de ellas responde si son ciertas o falsas las siguientes afirmaciones.
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso