2.2. El capital final
En el punto anterior hemos obtenido el dinero que habría acumulado Jorge, pero haciendo el proceso completo, año a año. Si fuesen muchos años esto nos complicaría bastante el proceso, ¿no?
|
|
|
| 12. Fuente propia |
13. Fuente propia |
Reflexionemos sobre otro ejemplo:
El hijo de Jorge, viendo que su padre ha conseguido un capital final bastante pequeño en el momento de jubilación, decide hacerse un plan de pensiones desde joven. Ahora tiene 25 años y se plantea aportar 500 € cada año, hasta su jubilación (a los 65 años), en una entidad financiera, en la que le ofrecen un 4 % de interés anual.
¿Cuánto dinero tendremos al final de esos t años?
| AÑO | EJEMPLO | GENERALIZACIÓN |
|
Primer año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
Recuerda que para obtener el capital acumulado a final de un período
basta con multiplicar el dinero disponible al principio del mismo por 1
más el interés en tanto por uno (es decir, el interés dividido por
100). Aquí, hemos llamado i al resultado de 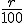 . . |
||
|
Segundo año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
|
Tercer año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
|
Insistimos en hacer notar que siempre, en cada paso, al capital acumulado le sumamos la aportación periódica y multiplicamos por 1+i. Observa la expresión teórica que da el capital en cada paso (fíjate en los sumandos que tiene, tantos como el número del período, y en los exponentes de (1+i)). Claro, seguir con este proceso hasta el final de esta operación (que durará 40 años) sería demasiado laborioso y pesado. Convendría tener una expresión para obtener el resultado sin hacer el cálculo todos los años. |
||
| Tras 40 años |
¿Qué capital tendrá este joven pasados los 40 años?. Vamos a intentar razonarlo sobre nuestro desarrollo teórico. | |
| TRAS t AÑOS |
Sabemos que el capital acumulado será la suma de lo aportado más los intereses generados. Si nos fijamos en lo que ha ocurrido en los 3 primeros años, la fórmula para el capital acumulado al cabo de t años sería:
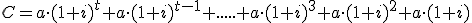
Como comentábamos antes, ha de tener t sumandos ya que hablamos de t años (todos los sumandos con el factor común a), y el primer sumando lleva el factor (1+i) elevado al número de años (t), el segundo a t-1, y así, bajando de exponente hasta quedarse en 1+i. Sin embargo, pensarás que si no se lo que hay en los puntos suspensivos cómo voy a sumar. No te preocupes, en realidad utilizando propiedades de las progresiones geométricas que no necesitas conocer (pero que podrás estudiar si lo deseas en "Para saber más...") se llega a la siguiente fórmula, que nos permite hacer el cálculo deseado:
|
|
Apliquemos la fórmula al plan de pensiones del hijo de Jorge:
|
APORTACIÓN PERIÓDICA: |
INTERÉS ANUAL: |
TIEMPO: |
| a = 500 € |
r = 4%
|
t = 40 años |
|
|
||
¿Qué capital habrá acumulado cuando se jubile?
Vamos a intentar resolver este problema utilizando la fórmula, no dando todos los pasos como en el apartado anterior.
La fórmula es:
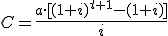
En nuestro problema tenemos: t = 5 años, i = 0,06 y a = 1000 €.
Resolvemos:
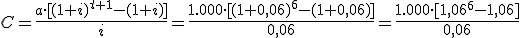
De donde:
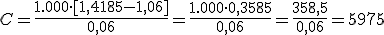
Progresiones Geométricas.
Una progresión geométrica es una sucesión de números en la que cada término es igual al anterior multiplicado por un número fijo llamado razón de la progresión.
Ejemplos:
a) 2, 4, 8, 16, 32, ..... (cuya razón es 2).
b) 27, 9, 3, 1, 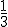 , ..... (cuya razón es
, ..... (cuya razón es 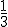 ).
).
Se llama término general de una progresión geométrica a una expresión que te permite hallar un término cualquiera de la progresión. Este término se obtiene con la fórmula:
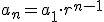
En los ejemplos anteriores:
a) En esta sucesión 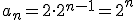 . Y así, el vigésimo término de esta sucesión sería:
. Y así, el vigésimo término de esta sucesión sería: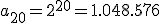 .
.
b) En este caso 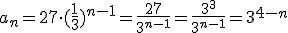 . Y el octavo término será:
. Y el octavo término será: 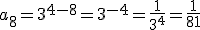
En una progresión geométrica es posible obtener la suma de n términos consecutivos de la misma. La expresión que nos permite obtener esta suma es:
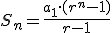
Si nos planteamos la suma de los 10 primeros términos de la progresión geométrica 2, 4, 8, 16, 32, ..... 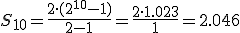 -
-
Utilizando la expresión anterior, de la suma de los n términos de una progresión geométrica, se obtiene la expresión que nos da el capital acumulado en una operación de capitalización.
En el siguiente enlace puedes ampliar más sobre progresiones aritméticas y geométricas.
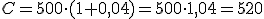 €
€
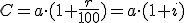 €
€
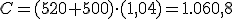
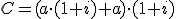
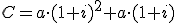 €
€
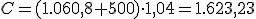 €
€
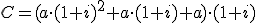
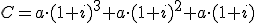 €
€
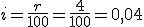
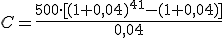
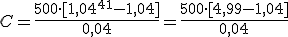
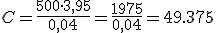

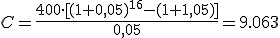 €.
€.