2. ¿Qué será de nosotros?
 |
 |
|
Vedere cadere le foglie, de Cinzia A. Rizzo,
|
Si miramos las hojas o las pisadas de estas fotos como si fueran puntos de nuestras gráficas, ¿podrías decir dónde caería la próxima hoja? ¿o dónde estaría la pisada que sigue el camino? En el primer caso sería mucha casualidad que acertaces, pues la correlación es nula. Sin embargo, en el segundo caso la correlación es muy fuerte y seguro que podrías dar una respuesta bastante ajustada.
Eso vamos a hacer en este apartado, predecir resultados a partir de los datos que tenemos. Ten en cuenta que esas predicciones serán más fiables cuanto mayor sea el coeficiente de correlación.
A lo largo de este tema y del anterior, has visto que en algunas gráficas aparecía una recta que se ajustaba a la nube de puntos. Esa línea se llama recta de regresión y es la recta que mejor se ajusta a la nube de puntos.
Curiosidad
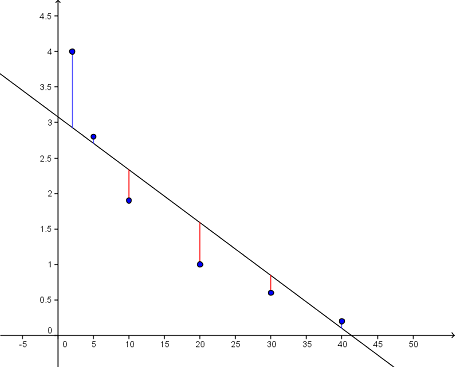¿Cómo se consigue la recta que mejor se ajusta? Fíjate en el gráfico de la derecha.
Si tomamos una recta cualquiera, medimos la distancia en vertical desde cada punto hasta la recta. Si el punto está por encima de la recta, el resultado es positivo (segmento azul), y si queda por debajo, el resultado es negativo (segmento rojo).
Lo que queremos es que la suma de esas distancias sea lo menor posible para que el ajuste sea mejor, pero si sumamos números positivos con negativos unos anularán a los otros.
Un método para conseguir que todas las distancias sean positivas es elevarlas al cuadrado. Ahora sí podemos sumar todos los resultados y buscar la recta que hace que esa suma sea lo menor posible.
Este método, que se llama Método de los mínimos cuadrados, es el que nos da la recta de regresión que vamos a estudiar en este apartado.
En la siguiente escena tienes un ejemplo de una nube de puntos y su recta de regresión (de color azul), así como otra recta (de color rojo) que hemos llamado aleatoria. Esta última recta la puedes cambiar moviendo los puntos rojos. En la escena también se expresa la aproximación que se consigue con cada recta de la nube de puntos.
Vamos a hacer un par de pruebas:
a) Mueve los puntos rojos e intenta hallar una mejor aproximación a la nube de puntos que la expresada por la recta de regresión. ¿Es posible encontrarla?
b) Si mueves los puntos azules, estarás modificando la nube de puntos y por tanto la recta de regresión. Modifica los puntos azules que quieras y repite el intento de mejorar la aproximación que viene dada por la recta de regresión.
Actividad
Para una variable estadística bidimensional, la recta de regresión de Y sobre X viene dada por la ecuación:
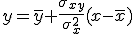
Una vez que tenemos la ecuación de la recta, podemos "predecir" valores de la variable que no conozcamos sustituyendo el valor de x. Veámoslo en el siguiente ejemplo.
Ejemplo o ejercicio resuelto
En el apartado anterior calculaste los parámetros para una Variable en la que se relacionaba el peso y la tensión arterial de los pacientes de un Centro de Salud.
Los valores que obtuviste fueron los siguientes: 
a) Calcula la recta de regresión de Y sobre X.
Como hemos visto, la recta de regresión de Y sobre X es la que mejor aproxima los valores de la variable Y a una recta, pero también podemos aproximar los valores de X. Para ello usamos otra recta, la recta de regresión de X sobre Y, que tiene la siguiente ecuación:
En la siguiente escena tienes la representación gráfica de las dos rectas. Cuanto más próximo sea el valor del Coeficiente de correlación de Pearson a 1 o -1, mayor coincidencia habrá entre ambas rectas. Puedes modificar los puntos para ver cómo varían ambas rectas.
El punto verde es el Centro de Gravedad de la distribución, y sus coordenadas son 
.
AV - Pregunta de Selección Múltiple
Utilizando los datos del Estudio B del apartado anterior, calcula las ecuaciones de las rectas de regresión de Y sobre X y de X sobre Y.
Recta de regresión de Y sobre X: y = 0,49x+1,02
| |
Recta de regresión de Y sobre X: y = 0,49x+2,01
| |
Recta de regresión de X sobre Y: x = 1,82y-3,16
| |
Recta de regresión de X sobre Y: x = 1,82y-1,36
| |
Curiosidad
Aunque hemos visto que la correlación indica que una variable esté relacionada con otra, esto no quiere decir que exista una relación de causa y efecto entre una y otra. Mira los siguientes ejemplos:
- Según la DGT, el 20% de los motoristas fallecidos en accidentes de tráfico no llevaban casco.
- La mayoría de los accidentes de tráfico se producen entre vehículos que ruedan a una velocidad moderada.
- Los días de luna llena se produce un aumento en el número de nacimientos.
- El cambio climático provoca el aumento de tornados en el hemisferio norte.
En el primer y segundo caso, no se puede establecer que sea mejor no llevar casco o circular a una velocidad excesiva, pues lo que no se dice es que la mayoría de los motoristas llevan casco, y la mayoría de los coches circulan a una velocidad moderada, de ahí que sea también mayor el número de accidentes.
El tercer ejemplo es el típico caso en el que, a pesar de haber sido refutadas con estudios estadísticos, siguen formando parte de las leyendas urbanas.
El cuarto, es un ejemplo de mal uso de las estadísticas para crear buenos titulares. Los estudios indican que, aunque haya aumentado el número de tornados en el hemisferio norte, no ha sido así a nivel mundial y no se puede establecer que el aumento de tornados sea causa directa del cambio climático.
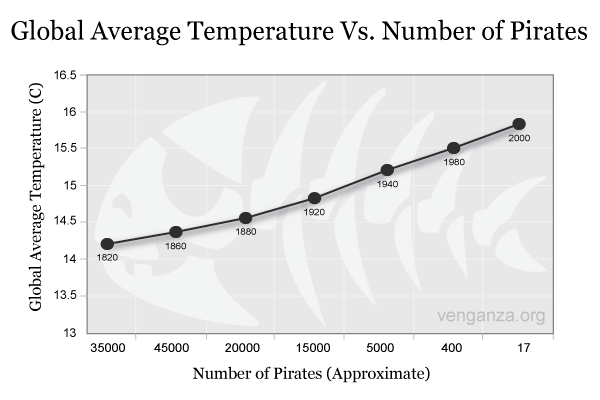
El gráfico que tienes arriba, de la web www.venganza.org, representa el aumento de las temperaturas globales y la disminución en el número de piratas en los últimos siglos. Es un ejemplo muy curioso de cómo se pueden relacionar dos variables que no tienen nada que ver, y obtener una correlación muy fuerte ¿Han desaparecido los piratas debido al cambio climático?
Resumiendo, como nos explican en Microsiervos, hay que aprender a interpretar los estudios estadísticos y a ser crítico con las noticias que nos llegan a diario.