1. Estamos compenetrados

¿Recuerdas las nubes de puntos del tema anterior? Con ellas podíamos determinar si había algún tipo de relación entre dos variables, y en ese caso decidir si la relación era positiva o negativa (al aumentar la primera, aumentaba o disminuía respectivamente la segunda).

Esta relación la definiremos como correlación. Y ésta puede ser:

  • Correlación funcional: si existe una relación funcional entre las variables X e Y. Es decir, podemos calcular los valores de Y a partir de los de X, con una función.
  • Correlación positiva o directa: existe cierta relación entre ambas variables, y al aumentar los valores de X también aumentan los de Y (primer gráfico).
  • Correlación negativa o inversa: existe cierta relación entre las variables, pero al aumentar los valores de X disminuyen los de Y (segundo gráfico).
  • Correlación nula: no existe ningún tipo de relación entre ambas.

 

Observa ahora las dos siguientes gráficas obtenidas al hacer el mismo estudio sobre dos poblaciones diferentes.

 

Como puedes ver, en ambas la correlación es positiva. Pero, ¿crees que en los dos casos existe la misma dependencia entre las variables? Por lo que se puede apreciar en las gráficas, en el Estudio A la dependencia parece ser más fuerte que en el Estudio B. Por tanto, debe existir alguna forma para medir la correlación.

A continuación, definiremos dos parámetros, la covarianza y el coeficiente de correlación lineal, que nos servirán para establecer esta medida.

Icono IDevice Importante

Antes de seguir, tienes que repasar algunas de las medidas que viste en el tema 2: la media y la desviación típica. Recuerda que si una variable X toma los valores x1, x2,... xn con frecuencias f1, f2,... fn, entonces:

  • La media se calcula:

 

 

 

  • En tanto que la desviación típica se halla:

Icono IDevice Pre-conocimiento

Recuerda, que el símbolo 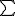se utiliza para indicar de forma abreviada la suma de varios números.

Por ejemplo, para acortar la siguiente suma x1 + x2 + x3 + x4, escribimos: .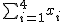

Si queremos abreviar la suma x1·f1 + x2·f2 + x3·f3 + ... + xn·fn, escribimos: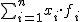


a) La Covarianza de una Variable Estadística Bidimensional (X,Y) la denotaremos como σxy y se calcula

donde fi es la frecuencia de cada par (xi,yi), N es el total de pares de valores y e son las medias marginales de cada variable.

 

Interpretación: el signo de la covarianza nos permitirá saber el tipo de correlación.

  • Si la covarianza es positiva, la correlación será directa.
  • Si la covarianza es negativa, la correlación será inversa.

En la siguiente presentación puedes ver cómo calcularemos la covarianza a partir de una tabla simple.

 

Covarianza

 

b) El Coeficiente de Correlación de Pearson es el parámetro que nos va a decir si la correlación es débil o fuerte. Para calcularlo, necesitamos conocer el valor de las desviaciones típicas marginales de cada variable σx y σy. Su valor siempre estará entre -1 y 1. Su expresión es la siguiente:

 

 

Interpretación: Según los valores de r, tenemos cuatro casos:

  • r = 0: No existe correlación.
  • r = 1 ó r = -1: La correlación es perfecta.
  • r próximo a 1 o -1: La correlación es fuerte.
  • r próximo a 0: La correlación es débil.

Veamos cómo calcularla con el ejemplo anterior.

 

Cálculo del Coeficiente de Correlación de Pearson

 

AV - Pregunta de Selección Múltiple
Vamos a recuperar los Estudios A y B del comienzo de este apartado. Vas a calcular el coeficiente de correlación de Pearson para comprobar si el resultado se corresponde con lo que habíamos supuesto por la gráfica.

Para realizar los cálculos te daremos la suma de los totales de cada columna, como en los ejemplos anteriores. El valor de N=104.

 

ESTUDIO A

xi

yi

xiyi

xi2

yi2

TOTALES

502,2

354,56

2165,43

3336,04

1437,21

 

 

ESTUDIO B

xi

yi

xiyi

xi2

yi2

TOTALES

502,2

353,83

2157,92

3336,04

1451,59

Observación: por cuestión de redondeo, puede que los resultados que te ofrecemos no coincidan exactamente con los tuyos. Elige los que más se aproximen.

a) ¿Cuáles de los siguientes valores corresponden a las medias marginales de X e Y para ambos estudios?

Estudio A: Media X = 4,83
Estudio B: Media Y = 4,53
Estudio A: Media Y = 3,41
Estudio B: Media X = 4,83



b) ¿Qué valores corresponden a las desviaciones típicas marginales de X e Y para esos dos estudios?

Estudio A: Desviación típica de X = 2,96
Estudio B: Desviación típica de Y = 2,15

Estudio A: Desviación típica de Y = 1,48
Estudio B: Desviación típica de X = 2,96



c) ¿Cuáles de las siguientes covarianzas corresponden a la de esos estudios?

Estudio A: Covarianza = 4,36
Estudio B: Covarianza = 4,32

Estudio A: Covarianza = 4,58
Estudio B: Covarianza = 4,52




d) Calcula los correspondientes Coeficientes de Correlación de Pearson.

Estudio A: r = 0,99
Estudio B: r = 0,95

Estudio A: r = 0,97
Estudio B: r = 0,91




e) Por último, a la vista de los resultados, podemos afirmar que:
Ambos estudios tienen correlación positiva, y la del Estudio A es más fuerte que la del Estudio B
Ambos estudios tienen correlación positiva, y la del Estudio A es más débil que la del Estudio B



« Anterior | Siguiente »