1.3. Agárrate que vienen curvas
Supongo que has observado el movimiento que describe el puente antes de derrumbarse. Esto es debido a un fenómeno llamado resonancia. Pero vayamos a cuestiones más sencillas, este movimiento de tipo ondulatorio podemos representarlo en los ejes coordenados a través de una familia de funciones llamadas funciones trigonométricas. A pesar de que esta familia es más extensa, nosotros estudiaremos únicamente la función seno, la función coseno y la función tangente.
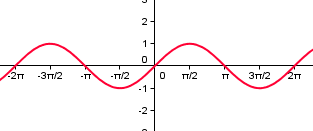
- La función seno es aquella función que a un número real x, le asocia el seno de ese número, es decir f(x)=sen x.
- La función coseno es aquella función que a un número real x, le asocia el coseno de ese número, es decir f(x)=cos x.
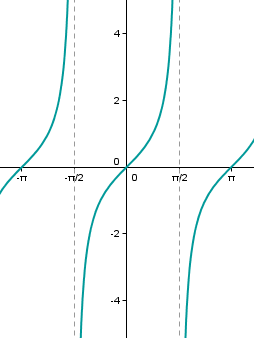
- La función tangente es aquella función que a un número real x, le asocia la tangente de ese número, es decir f(x)=tg x.
 |
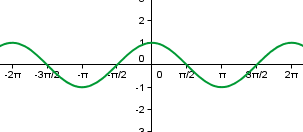 |
| f(x)=sen (x) | g(x)=cos (x) |
Y completa sus propiedades con los siguientes términos: decreciente, par, creciente, periódicas, -1, R, impar, 1.
- El dominio de ambas funciones coincide y es .
- El recorrido de ambas es [ , ].
- Son de periodo 2∏.
- Monotonía: La función seno, es en los intervalos [0,∏/2] y [3∏/2,2∏], y en [∏/2,3∏/2]. La función coseno es de [∏,2∏] y de [0,∏].
- Simetría: La función seno tiene una simetría y la coseno una simetría .
|
|
| f(x) | g(x) |
Una de estas gráficas corresponde a la tangente, ¿cuál? Recuerda que la tangente es el cociente entre el seno y el coseno.
|
La función f | |
|
La función g
|
- El dominio de esta función son los números reales excepto los múltiplos de ∏/2.
- Su recorrido, todos los números reales.
- Es periódica de periodo ∏.
- Es creciente en todo su dominio.
- Tiene una simetría impar.
Desde el punto de vista matemático las gráficas de las funciones seno y coseno son formas perfectas, paradigmáticas, de bellas y armoniosas ondas. A partir de ellas se construyen los demás movimientos “armónicos”. Destacan por su periodicidad y repetición cíclica.
Muchos fenómenos que se observan en la naturaleza son periódicos y revisten carácter cíclico. La vida está medida y gobernada por la sucesión de días y noches, veranos, inviernos, años... El cuerpo humano está constantemente animado por ritmos fisiológicos, latidos, respiraciones... Las máquinas que el hombre inventa están gobernadas por la repetición a intervalos regulares de tiempo, incluso la actividad social, como la música, o las elecciones democráticas tienen también su ritmo cíclico.
 |

|
 |
|
y=cos(x) por kenwood |
undulating por shindohd CC by-nc-sa 2.0 |
undulations por wanderignone CC by-nc-nd 2.0 |
Fíjate en las tres fotos anteriores, y en sus títulos. En las dos últimas se aprecia claramente la relación existente entre ellas y las funciones trigonométricas, sin embargo la primera que a priori es diferente tiene un título más explícito... ¿cuál será la relación existente entre esta imagen y nuestra función coseno?
La respuesta la encontramos en el siguiente artículo del diario el Mundo:
"Desde abajo, la torre arranca con una base cuadrada y a medida que se eleva va perdiendo sección, esa pérdida va generando una curva que matemáticamente representa la función y=coseno de x"
Por cierto, igual has reconocido en esta foto al edificio madrileño Torre Espacio.
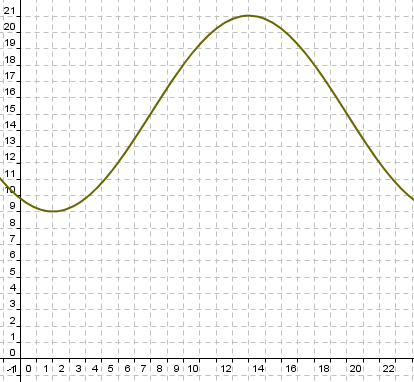
donde t es el tiempo medido en horas desde la medianoche.
- ¿Cuál es la temperatura a las 8 h, a las 12 h y a las 6 de la tarde?
- Representa gráficamente la función.