1.1. ¿Manzanas podridas en el laboratorio?
Albert A. Barlett (1923) eminente profesor de Física de la Universidad de Colorado aseguró en cierta ocasión
"El mayor defecto de la raza humana es nuestra incapacidad para comprender la función exponencial"
¿Podremos demostrarle al fabuloso profesor que carecemos de dicho defecto? ¿O será nuestra primera manzana podrida en nuestro particular laboratorio?
Eso sí, hasta el famoso humorista gráfico Forges desconfía de la sencillez de dicha función...
 |
| Viñeta de Forges tomada de www.actiludis.com |
| x | f(x)=x2 |
g(x)=2x |
| 0 | ||
| 1 | ||
| -1 | ||
| 2 | ||
| 10 |
La anterior escena de GeoGebra permite representar las funciones exponenciales f(x)=ax. Ayúdate de ella para completar los siguientes espacios en blanco, donde se expresan algunas propiedades de este tipo de funciones.
- Para que f sea una función exponencial a no puede ser ni 0 ni , pues para esos valores la funión es una semirecta y una recta respectivamente.
- El dominio de la función exponencial no depende de a y es
- La imagen de 0 siempre vale
- La función es creciente si a es mayor que
- La función es decreciente si a es menor que
- f tiene una asíntota horizontal en .
 |
|
Microscopy work por kasi metcalfe CC by-nc-nd 2.0
|
Algunas bacterias se reproducen por mitosis, es decir, se dividen en dos cada pequeño intervalo de tiempo, dejando la misma carga de ADN en ambas partes. Vamos a imaginar que trabajamos en un laboratorio y estamos estudiando este tipo de bacterias. No es que la vida de millones de personas dependa de nosotros, pero formamos parte de un proyecto secreto...
Si estas bacterias se dividen cada 15 minutos y al principio del día sólo hay una ¿cuántas habrá al final del día?
 |
|
Euler por imago CC by-nc-sa 2. |
En el tema anterior hemos visto la suma de funciones, si una de las funciones es una constante, el efecto que se produce al sumarla a otra función es un desplazamiento o traslación de su gráfica.
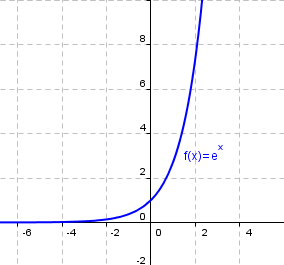
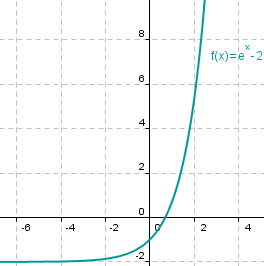
En las dos imágenes siguientes se puede apreciar cómo se ha desplazado la gráfica de la función f(x)=ex al restarle la función constante 2, g(x)=2.
 |
 |
En las siguientes tablas, vamos a recoger algunos valores de las siguientes funciones exponenciales: y=5x, y=5x+3, y=5x-2, y=5x+3, y=5x-2.
| x | y=5x |
y=5x +3 |
y=5x -2 |
| -2 | |||
| -1 | |||
| 0 |
|
||
| 1 | |||
| 2 |
| x | y=5x | y=5x+3 | y=5x-2 |
| -2 |
|
||
| -1 | |||
| 0 | |||
| 1 | |||
| 2 |
Al representar las funciones y=5x+3 e y=5x-2 se observa que son traslaciones de la gráfica y=5x.
Al representar las funciones y=5x+3 e y=5x-2 se observa que son traslaciones de la gráfica y=5x.