2. Segundo acto
 |
¿Cómo llevas la obra de teatro? ¿Bien? ¿Te ha resultado muy largo el primer acto o, por el contrario, te ha parecido ameno?
Bueno, ya queda menos. Casi sin darnos cuenta, ya estamos en el segundo acto, en mitad del tema. En el primero hemos hablado de monotonía, extremos y puntos de corte.
En éste, trataremos otras características de interés a la hora de estudiar y analizar funciones y gráficas.
· Una función es simétrica respecto al eje de ordenadas (OY), si para todo valor, x, de su dominio se cumple que: f(-x)=f(x). En este caso decimos que la función es Par.
· Una función es simétrica respecto al origen de coordenadas, si para todo valor, x, de su dominio se cumple que: f(-x)=-f(x). En este caso decimos que la función es Impar.
Aunque existen funciones de los dos tipos descritos, Par e Impar, lo más frecuente es que una función no presente ningún tipo de simetría.
|
Proyecto edad. ITE. Ministerio de Educación
|
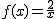 ,
,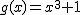 y
y 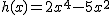
- f(x) es una función simétrica respecto del de , luego es una función .
- D(f)=
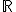 -{
}
-{
} - R(f)=
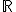 -{
}
-{
} - En cuanto a su monotonía, podemos afirmar que f(x) es una función .
- ¿g es par? ¿g es impar?
- g(x) corta al eje OY en el punto ( , )
- ¿h es par? ¿h es impar?
- La gráfica de h(x) corta al eje OX en (0,1,2,3 ó 4) puntos distintos.

|
| Imagen de yosoyjulito con licencia CC BY 2 |
Simetría - Paridad
Nuestro cuerpo y nuestra cara son simétricos respecto a un eje de simetría imaginario que pasa por nuestra nariz y nuestro ombligo.
Pero la cara, además, presenta una simetría especial porque podríamos dibujar una parábola alrededor de ella cuyo vértice estaría en la punta de nuestra barbilla.
¿Te atreves a dibujarla con Geogebra?
Puedes hacer uso del siguiente recurso:
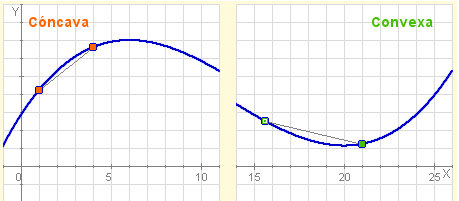
· Una función, f, es cóncava en un intervalo determinado si el segmento que une dos puntos cualesquiera de la curva en dicho intervalo queda por debajo de la gráfica de f y es convexa si queda por encima.
· Los puntos del dominio en los que la función, f, pasa de cóncava a convexa, o viceversa, reciben el nombre de puntos de inflexión.
Vamos a analizar de manera detallada la siguiente gráfica.
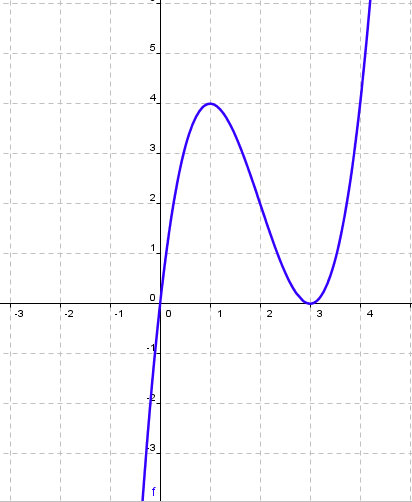
(a) ¿Con qué ecuación crees que se corresponde el dibujo?
|
f(x) = 3x + 3
| |
|
f(x)= x3 - 6x2 + 9x
| |
|
f(x)= 5x2 + 3
|
(b) Es decreciente en:
|
el intervalo (1,3)
| |
|
el intervalo (0,3)
| |
|
ningún intervalo. Es siempre creciente.
|
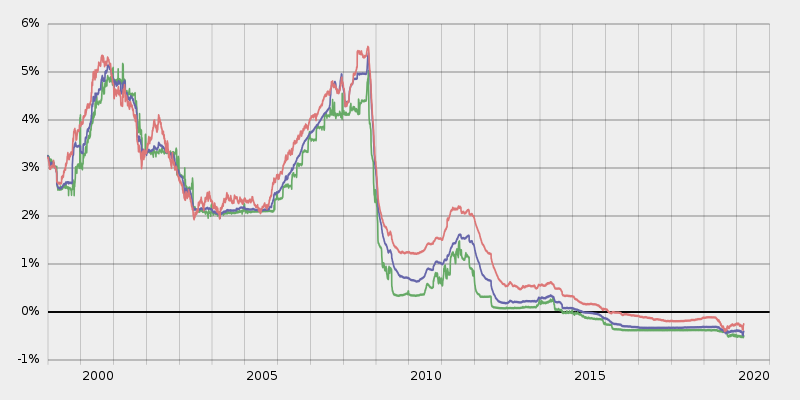 |
El concepto de tendencia en campos como la economía tiene mucha relevancia, es indicativo o premonitorio de que algún fenómeno económico se va a comportar, o al menos se espera que se comporte de una manera determinada.
Continuamente oímos expresiones como "la bolsa de Madrid ha cerrado hoy con una tendencia al alza y el IBEX 35 ha subido ..."
Sobre tendencias y límites de funciones hablaremos más detenidamente en la próxima unidad. Solamente, de momento, conviene que sepas a que se refiere.
En la imagen se observa como el Euribor lleva bastante tiempo en mínimos históricos, por lo que lo más normal es que no aguante mucho tiempo más así y presente una tendencia al alza. En definitiva, que se espera que aumente su valor y por tanto el de nuestras hipotecas. Por consiguiente, pagaremos más cada mes y, por tanto, tendremos menos dinero para gastar en otras cosas.
Conclusión: Cuando oigas que el Euribor, tiene tendencia al alza, ¡vete preparando y dirige tus ruegos a quien confíes, porque tocará apretarse el cinturón!

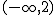 y cóncava en el intervalo
y cóncava en el intervalo