1. Se levanta el telón
Actividad
Se define función real de variable real, a una relación que asocia a un número x de un conjunto inicial, otro número y de un conjunto final. El número y es único, es decir, a x no se le puede asociar más de un número.
A las funciones se les suele llamar f, y la relación se expresa de la siguiente manera: y = f(x).
Por ejemplo: La relación que existe entre la velocidad y el combustible consumido es una función, pues a cada velocidad sólo le corresponde una única cantidad de litros consumidos.
Definida así, matemáticamente, quizás no seamos capaces de ver todo el potencial que tienen las funciones. Pero, ¿y si las vemos representadas? Es decir, ¿y si vemos su gráfica?
En el siguiente vídeo se muestra el porqué de la utilización masiva de las gráficas en distintas áreas del conocimiento, no sólo en matemáticas, mediante una batería de ejemplos de la vida cotidiana. Se describe el nacimiento del lenguaje de las gráficas, se presenta la relación: ecuación de una función-gráfica y se muestra donde radica el verdadero potencial de estos objetos:
"Ante todo, una gráfica es capaz de ofrecer un gran volumen de información, tanto numérica como cualitativa de una manera global, es decir, de un simple vistazo" (Antonio Pérez Sanz).
Se ha levantado el telón. En este primer acto estudiaremos algunas de las características de las funciones. Comenzaremos estudiando su monotonía (crecimiento y decrecimiento).
Algo que realizamos con mucha frecuencia es estudiar el comportamiento, la evolución, de cualquier fenómeno de la realidad. El impacto que ha tenido una determinada película en su lanzamiento se mide en función del número de espectadores que acuden a verla en las salas de cine. Si representásemos esta función, sea cual sea la película, es más que probable que se comporte de esta manera: en su inicio será creciente, posteriormente con el paso del tiempo se estanca, a lo mejor se recupera un poco, para acabar bajando cada vez más en número de espectadores hasta que no sea rentable su proyección y desaparezca de la cartelera.
Importante
Atendiendo a la monotonía podemos clasificar las funciones en tres tipos.
· Una función real f(x) es creciente en un intervalo si para dos valores cualesquiera del intervalo x y x', con x < x', se tiene que: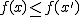 
· Una función real f(x) es decreciente en un intervalo si para dos valores cualesquiera del intervalo x y x', con x < x', se tiene que: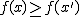 
· Una función real f(x) es constante en un intervalo si para todos los valores, x, del intervalo se tiene que: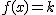 
(constante)
Aunque existen funciones que son crecientes, decrecientes o constantes en todo su dominio de definición, lo más habitual es encontrarse con aquellas que tienen una combinación de todos los tipos indicados.
Pero, no basta con conocer si una función crece o decrece. En ocasiones nos interesará conocer hasta dónde llega ese crecimiento y/o decrecimiento, si se alcanzan máximos/mínimos absolutos, o si los valores obtenidos son extremos relativos, es decir, son grandes o pequeños, sólo en comparación con los que tienen a su alrededor.
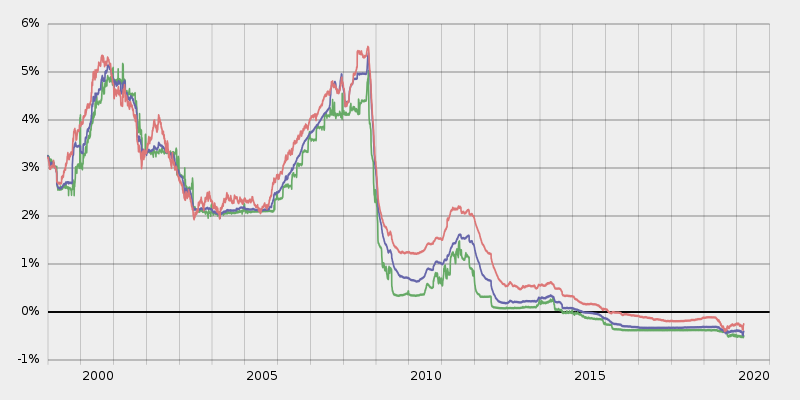
Seguro, que en alguna ocasión has oído hablar del Euribor. La actualización de las cuotas que pagamos por los préstamos hipotecarios se realiza en base a este índice de referencia. Cuanto más alto (bajo) sea su valor, mayor (menor) será la cantidad que debamos pagar mensualmente por nuestra hipoteca. En la imagen se observan altibajos de crecimiento y decrecimiento y algunos puntos, valores, que llaman la atención bien por ser los más altos o los más bajos. Son los que denominamos extremos. A continuación, hablaremos de ellos.
 |
Actividad
Extremos absolutos.
· Una función f alcanza su máximo absoluto en el punto x=a si es creciente a la izquierda de este punto y decreciente a su derecha. El valor de la ordenada (coordenada y) en el máximo es mayor o igual que en cualquier otro punto del dominio de la función.
· Una función f alcanza su mínimo absoluto en el punto x=b si es decreciente a la izquierda de este punto y creciente a su derecha. El valor de la ordenada (coordenada y) en el mínimo es menor o igual que en cualquier otro punto del dominio de la función.
Pero, en ocasiones, hay otros puntos que destacan entre los de su entorno más cercano, son los:
Extremos relativos.
· Una función f tiene un máximo relativo en el punto x=a si f(a) es mayor o igual que en todos los puntos próximos al punto x=a, tanto por la derecha como por la izquierda de él.
· Una función f tiene un mínimo relativo en el punto x=b si f(b) es menor o igual que en todos los puntos próximos al punto x=b, tanto por la derecha como por la izquierda de él.
Del mismo modo que hay puntos importantes como los extremos, existen otros que presentan una singularidad especial. Son los puntos de cortes con los ejes.
Importante
Llamamos puntos de corte a aquellos puntos en los cuales la gráfica representada corta al eje de abcisas (eje OX) y/o al de ordenadas (eje OY).
- Los puntos de corte con el eje OX son de la forma (x0,0). Su coordenada y vale 0.
- Los puntos de corte con el eje OY son de la forma (0,y0). Su coordenada x vale 0.
Si tenemos la ecuación de la función en la forma y = f(x), hallar los puntos de corte:
· Con el eje OX, equivale a resolver el sistema de ecuaciones: {y=f(x), y=0}
· Con el eje OY, equivale a resolver el sistema de ecuaciones: {y=f(x), x=0}
AV - Actividad de Espacios en Blanco
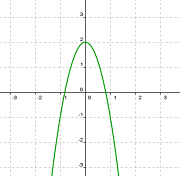
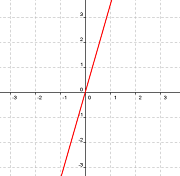
Observa con detenimiento las gráficas de las funciones representadas y rellena a continuación los huecos en cada una de los apartados:
 |
 |
| Gráfica 1 |
Gráfica 2 |
Llamaremos f(x) a la función representada en la Gráfica 1 y g(x) a la representada en la Gráfica 2.
· f(-1) = , f( ) = 2 , f(1) =
· f es una función
en el intervalo (-
,0] porque -1
0 y f(-1) ≤ f (0)
· f es una función
en el intervalo [
,+) porque
<
y f(0) ≥ f (1)
· f corta al eje OY en el punto de coordenadas ( , )
· f corta al eje OX en punto/s
· g es una función estrictamente
· g(0) =
· g corta el eje OX en el punto ( , ) y al eje OY en el punto ( , )
Ejemplo o ejercicio resuelto
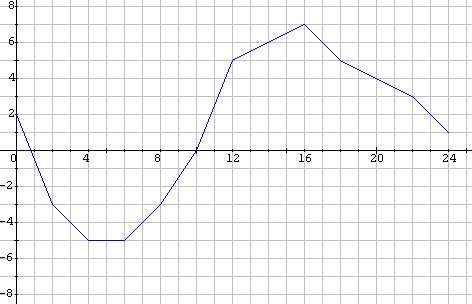
En la siguiente imagen puedes ver la gráfica de las temperaturas a lo largo de un día en una ciudad española. En el eje OX están representadas las horas del día y en el eje OY las temperaturas en grados centígrados.
Horas del día - Temperaturas (ºC)
(a) ¿Qué temperatura hizo a las 0 horas? ¿Y a las 10 horas? ¿Son esos puntos significativos?
(b) ¿Qué se podría afirmar acerca del crecimiento y decrecimiento de la temperatura (monotonía)?
(c) ¿Se mantuvo constante la temperatura en algún intervalo del día? ¿Cual fue el valor de la temperatura en dicho intervalo?
(d) ¿A qué hora se alcanzaron las temperaturas máximas y mínimas? ¿Cuales fueron los valores de dichas temperaturas?
(e) ¿Son máximos/mínimos absolutos o relativos?
(f) ¿En qué tramo horario se alcanzaron temperaturas bajo cero?
Curiosidad
La cuenta de resultados.
|
|
Imagen de Eric Caballero con licencia CC BY
|
Si llamamos f(x): función de beneficios (ingresos menos costes) de una empresa, donde x representa el tiempo transcurrido en años desde su fundación.
(a) f(0) punto de corte con el eje OY, nos indicará el coste de la empresa. Es decir, al comienzo no existen ingresos luego, nos devolverá, cuánto ha sido la inversión necesaria para poner en marcha la empresa.
(b) Si para algún año, x, tenemos que f(x)=0, punto de corte con el eje OX, nos indicará que en el año x, la empresa ha obtenido un beneficio igual a 0 €. Ha ingresado lo mismo que ha gastado.
(c) Si f(x) > 0 indicará que la empresa ha obtenido beneficios. Por el contrario, si f(x) < 0 indicará que la empresa ha obtenido pérdidas durante ese año.