3.2. Viaje en barco

|
|
falucas y pescadores por Xavier Fargas bajo licencia CC by-nc-nd 2.0
|
"Sinuhé, en uno de mis últimos viajes por el Nilo, camino del oasis de El Fayum, nuestro barco sufrió la ira de Seth (dios de las tormentas), y el mastil quedó dañado y hubo que apuntalarlo, fijándolo a la popa y la proa. El barco tiene de eslora unos 30 metros, y las cuerdas formaron dos ángulos de 30º y 45º aproximadamente. ¿Podríamos calcular las longitudes de sendas cuerdas?"
Para resolver un triángulo donde conocemos un lado, a, y sus dos ángulos adyacentes B y C, debemos calcular los lados b y c, y el ángulo A.
En este caso la única limitación es que la suma de los dos ángulos no puede ser superior a 180º (para que pueda ser un triángulo).
Para calcular el ángulo que nos falta, utilizamos la propiedad que nos relaciona los tres ángulos de un triángulo. En cuanto a los lados, debemos utilizar el teorema del seno, ya que nos relaciona los dos lados de un triángulo con los dos ángulos opuestos correspondientes.
| SUMA DE LOS ÁNGULOS | TEOREMA DEL SENO |
TEOREMA DEL SENO |
|
|
|
|
Construir un triángulo conocidos dos ángulos adyacentes a un lado es muy sencillo. Observa el siguiente video
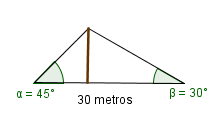 Llamémos A al ángulo que forman las dos cuerdas
Llamémos A al ángulo que forman las dos cuerdas