2.1. Si no es el Seno...
|
| Puzzle por INTVGene bajo licencia CC by sa-2.0 |
Resolver un triángulo implica conocer sus tres lados y sus tres ángulos. A primera vista, al contemplar un triángulo, no parece que exista mucha relación entre estos seis elementos. Sin embargo las matemáticas se presentan como una herramienta útil y elegante para unir las seis piezas de este puzzle.
La primera de ellas es el Teorema del Seno.
Actividad
En cualquier triángulo de ángulos A, B y C, y lados a, b, c, se cumple que
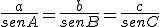
en la siguiente escena, mueve los vértices del triángulo, y así podrás comprobar cómo se cumple el teorema anterior.
Actividad de Espacios en Blanco
Vamos a completar las siguientes afirmaciones sobre este triángulo:
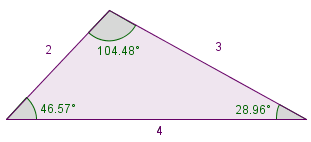
- El teorema del seno relaciona cada lado con su ángulo .
- En nuestro triángulo el lado de dimensión 4, se relaciona con el ángulo que mide º, y esta relación es de .
- En nuestro triángulo el lado de dimensión , se relaciona con el ángulo que mide 46,57º, y esta relación es de .
- Por lo tanto, la relación existente entre el lado de dimensión 2, y el ángulo 28,96º es de .
Objetivos
La demostración del Teorema del seno es muy sencilla, puedes echarle un vistazo en el siguiente video:
Actividad
El teorema del seno permite determinar la longitud de uno de los lados de un triángulo, conociendo:
- El ángulo opuesto al lado que queremos calcular
- Otro lado
- El ángulo opuesto a este lado
Reflexión
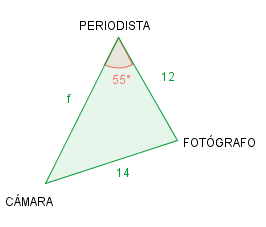
Debido a un incendio, los bomberos han cerrado una zona triangular de la calle. Un periódico decide enviar a unos reporteros (un periodista, un cámara, y un fotógrafo) para cubrir la noticia. Cada uno se sitúa estratégicamente en cada vértice del triángulo. Si la distancia entre el periodista y el fotógrafo es de 12 metros y la que separa al fotógrafo y al cámara es de 14 metros, ¿qué distancia ha de recorrer el periodista para ponerse en contacto con el cámara para hacer la conexión en directo? Hay que tener en cuenta que el ángulo en el que se encuentra el periodista es de 55º.
