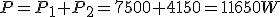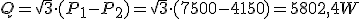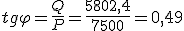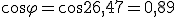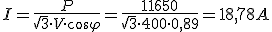3.2. Potencia en sistemas desequilibrados
 |
|
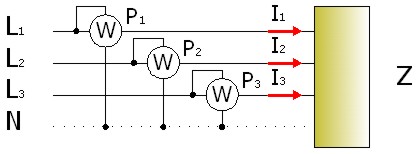
Imagen 24: Método de los tres vatímetros. |
 |
|
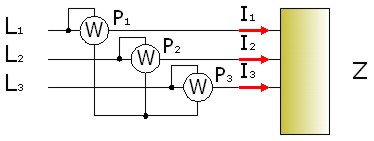
Imagen 25: Método de los tres vatímetros sin neutro. |
 |
|
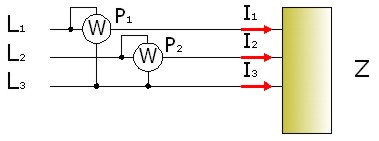
Imagen 26: Conexión Aron en sistema desequilibrado. |
Cada vatímetro toma la intensidad de la fase a la que se ha conectado y la tensión entre su fase y la tercera. Así podremos obtener la potencia total. Veamos como:
Sabemos que en cualquier sistema los valores instantáneos de potencia e intensidad son:
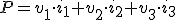 |
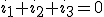 |
Puesto que el valor de i3 no lo medimos, podemos despejarlo en función de las otras dos intensidades:
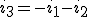 |
Y al sustituir en la expresión de la potencia nos quedará:
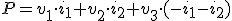 |
Si ahora agrupamos términos, nos quedará:
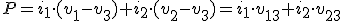 |
Es decir, la potencia total del sistema se puede conocer si sabemos la intensidad de dos de sus líneas y la tensión entre esas líneas y la tercera, que es precisamente la lectura que nos están ofreciendo los vatímetros que hemos conectado.
 |
|
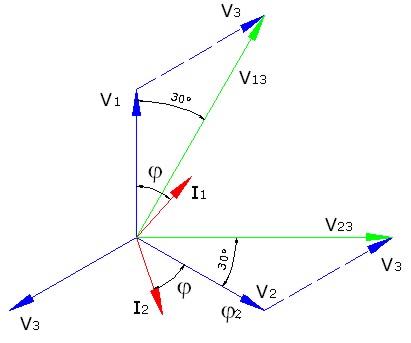
Imagen 27: Diagrama de tensiones en el método Aron. |
Tendremos que la expresión de la potencia la podemos escribir de la siguiente manera, según se observa en el diagrama vectorial:
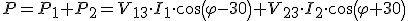 |
Y puesto que en este caso se trata de sistemas equilibrados tendremos que:
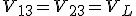 |
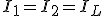 |
Por lo que la expresión de la potencia nos quedará:
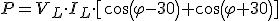 |
Si repasas la trigonometría que estudiaste en cursos anteriores, llegarás a la conclusión de que:
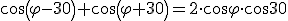 |
Por lo que la expresión de la potencia quedará:
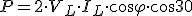 |
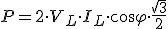 |
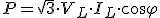 |
Y esta expresión nos da la potencia activa en un sistema trifásico.
Si en vez de sumar las potencias de los vatímetros P1 y P2 las restamos, y razonamos de forma similar a como lo hemos hecho obtenemos:
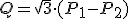 |
Esta expresión nos dice que la diferencia entre los vatímetros multiplicada por raíz de tres nos da la potencia reactiva.
Para finalizar, decir que los dos vatímetros se pueden conectar a dos cualesquiera de las líneas, siempre que sea de la forma que se ha indicado y que también se pueden utilizar con transformadores cuando la corriente de la línea sea elevada.