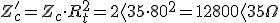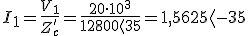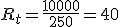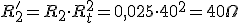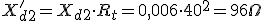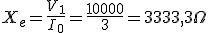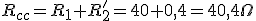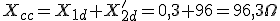3.3. Circuito equivalente y reducción de un transformador

Hemos visto que la relación de transformación puede tomar múltiples valores, ampliando o reduciendo las tensiones o intensidades decenas o incluso cientos de veces. Si, por ejemplo, consideramos un transformador elevador, y representamos vectorialmente las tensiones, como hemos hecho anteriormente, al tomar como referente las del primario ocurrirá que las del secundario serán decenas o cientos de veces mayores y gráficamente su representación sería un gran problema pues los vectores serían muy grandes. Para solucionarlo se recurre a la reducción del primario al secundario.
La manera de proceder consiste en dejar los vectores de las magnitudes del primario tal cual están y los vectores de las magnitudes del secundario se representan multiplicados por la relación de transformación Rt , de esta manera los vectores del secundario pasan a ser iguales que los del primario en módulo. Estos nuevos vectores los diferenciaremos, al igual que hacíamos con la intensidad reflejada en el primario, marcándoles como primos. Par que se entienda:

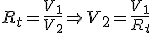
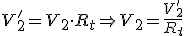
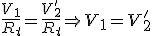Observando las expresiones anteriores vemos que V2 reducido al primario será V'2 , que como se ha dicho resulta de multiplicar V2 por Rt , y tiene el mismo valor que V1 , como puede verse en la tercera expresión.

Si procedemos de la misma manera con la tensión inducida en el secundario tendremos:


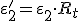Para el caso de la intensidad será:


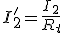También se pueden reducir al primario las caídas de tensión en R2 y X2d:

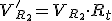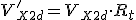La impedancia de carga conectada al secundario es un caso especial:


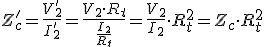Esto mismo podemos hacerlo con los valores de R2 y Xd2 del secundario, si queremos reducirlos al primario.

Por último, indicar que las potencias en el primario y en el secundario son iguales como ya se ha visto y los ángulos también son los mismos.

Esta actuación supone considerar un transformador con una relación de transformación que es la unidad y los vectores así obtenidos estarán representados a la escala Rt.

Veamos un ejemplo de aplicación.

Icono de iDevice Ejemplo o ejercicio resuelto
Para el ejercicio del apartado 1.3.2 ¿Cuál será la impedancia de la carga vista desde el primario?, ¿Cuál será la corriente que circule por el primario?

Si aplicamos a un transformador la reducción de las magnitudes del secundario al primario, tal y como hemos indicado más arriba, el esquema que obtendremos del transformador será el que indica la figura.

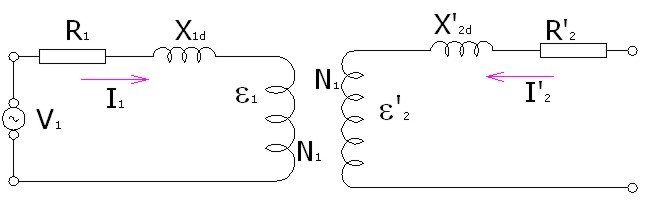Imagen 25: Esquema de un transformador con el secundario reducido al primario

Elaboración propia

Puesto que ε'2 tiene el mismo valor que ε1 entonces los arrollamientos actuarían como si tuvieran el mismo número de espiras y podríamos considerar unidos los puntos de comienzo y final de ambas bobinas, más aún, podríamos prescindir de una de ellas.


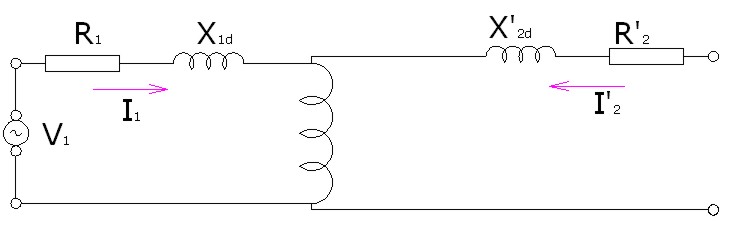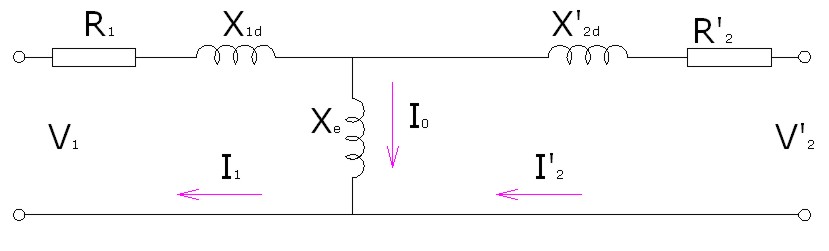
Imagen 26: Circuito equivalente de un transformador con el secundario reducido al primario

Elaboración propia

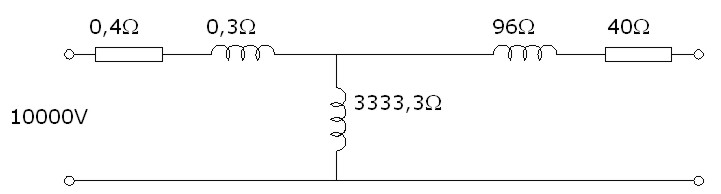
El esquema aún se podría simplificar más, ya que la corriente del primario era la suma de la corriente en vacío I0 más la reflejada del secundario I'2 (recordemos que tenía signo contrario).



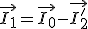Imagen 27: Circuito equivalente de un transformador con el secundario reducido a primario

Elaboración propia
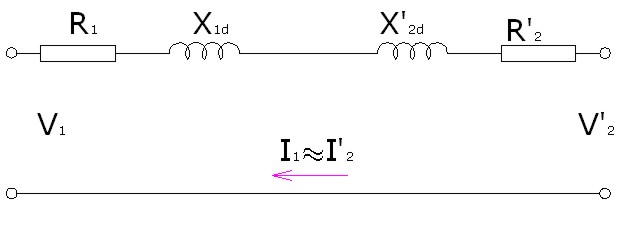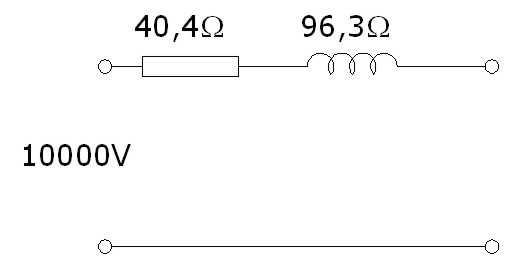
Por último, si resulta que I0«I1 , entonces I1≈I'2 por lo que obtenemos así el circuito equivalente simplificado que muestra la figura inferior.

Imagen 28: Circuito simplificado de un transformador

Elaboración propia

De este último esquema obtenemos algunas conclusiones:
Resistencia de cortocircuito Rcc
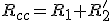
Reactancia de cortocircuito Xcc
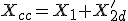Reactancia equivalente Xe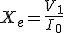
Apliquémoslo a un ejemplo:
Icono de iDevice Ejemplo o ejercicio resuelto
Tenemos un transformador con una relación 10000/250 V. De él conocemos R1= 0,4 Ω, Xd1= 0,3 Ω, R2= 0,025 Ω, Xd2= 0,06 Ω, I0= 3 A. Hallar el esquema equivalente así como la resistencia y reactancia de cortocircuito.
Repasa los conceptos de este apartado y verás que no es tan difícil.

Icono IDevice Objetivos
Es interesante que sepas que en la práctica, el circuito equivalente así obtenido nos permite conocer las tensiones e intensidades en aquellos circuitos en los que hay intercalado un transformador.

« Anterior | Siguiente »