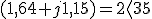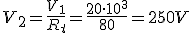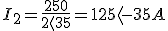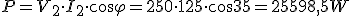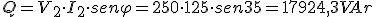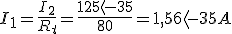3.2. El transformador real
Desde el comienzo del tema venimos considerando al transformador como una máquina ideal, carente de pérdidas de energía, pero nada más lejos de la realidad. Esas pérdidas, aunque pequeñas, se producen en forma de calor. Hasta ahora hemos supuesto:
- Que los conductores de las bobinas carecen de resistencia, pero lo cierto es que poseen esa resistencia que como ya sabemos depende de la resistividad del material, de su longitud y de su sección.
- Que no se producen efectos de dispersión de flujo magnético y eso no es cierto. Ni la permeabilidad del núcleo es infinita ni la del medio circundante (aire o aceite normalmente) es nula, por lo que siempre existirá un flujo de fugas en cada bobina que no circulará por el núcleo.
- Que en el material magnético utilizado en el núcleo no se producían efectos de histéresis ni corrientes de Foucault, y eso tampoco es cierto, pues siempre que se aplique un flujo al núcleo habrá pérdidas en el hierro.
Así pues, tenemos que considerar estas pérdidas y ver qué efectos producen para que así, nuestro transformador se aproxime lo más posible a la realidad. Para ello, primero analizaremos nuestro transformador funcionando en vacío:
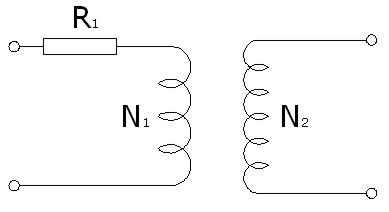
- Los conductores no son ideales, por lo que tienen resistencia eléctrica. Podemos suponer que las bobinas sigan siendo ideales, y para ello su valor resistivo estará concentrado fuera de la bobina en serie, tal como indica la imagen.
 |
|
Imagen 19: Resistencia de las bobinas
Elaboración propia |
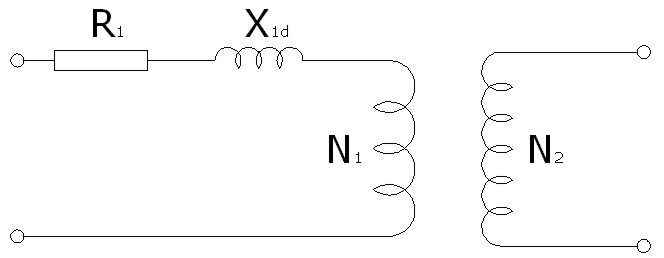
- Si ahora consideramos las pérdidas de flujo, tendremos que el flujo que afecta a la bobina del primario Φ1 estará formado por una parte que es común a ambas bobinas Φ y otra parte que es propia de cada bobina y que se debe a la dispersión Φ1d , es decir:
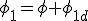 |
 |
|
Imagen 20: Esquema del transformador real en vacío
Elaboración propia |
- Por último, nos queda considerar las pérdidas en el hierro. En un transformador, al igual que en cualquier máquina eléctrica, al producirse un flujo variable, el material del núcleo se ve sometido a cambios continuos de imantación, que provoca rozamientos a nivel molecular y por lo tanto un calentamiento. De igual manera, aunque el núcleo del transformador está constituido por láminas para minimizar las corrientes de Foucault que se manifiestan sobre todo cuando la sección es considerable, es cierto que estas corrientes cerradas sobre si mismas se presentarán y eso provocará también pérdidas en el hierro.
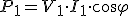 |
| Como cosφ=cosπ/2=0; entonces P1=0 |
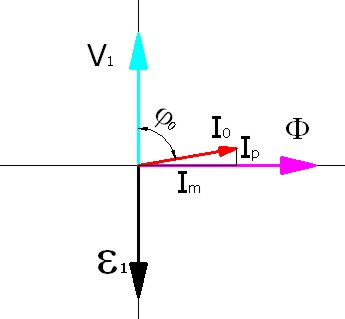
Pero acabamos de ver que la realidad no es esa. Cuando el transformador está en vacío, los efectos de magnetización del núcleo provocan un calentamiento del mismo, calor que resulta de la energía eléctrica absorbida por el primario y que en la práctica se traducen en que esa corriente de magnetización no se encuentra desfasada φ=π/2, sino un ángulo φ0≠90º.
Podemos representar esto vectorialmente, tal como indica la imagen y observamos que de la corriente absorbida, solo una parte tiene efectos magnetizantes Im y el resto son pérdidas Ip , ambas componen la corriente total absorbida I0.
 |
|
Imagen 21: Desfase de I0 en un transformador real en vacío Elaboración propia |
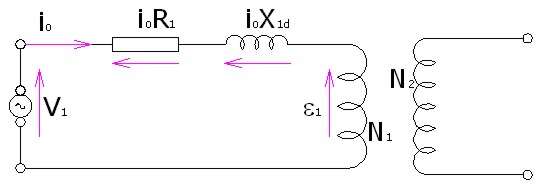
Habiendo analizado las pérdidas en un transformador, ya solo queda saber en qué se traducen. Para ello consideraremos el esquema siguiente, casi idéntico al estudiado anteriormente.
 |
|
Imagen 22: Esquema de modelo de transformador real
Elaboración propia |
Vectorialmente, la tensión en el primario será:
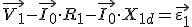 |
Y escalarmente será:
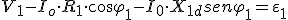 |
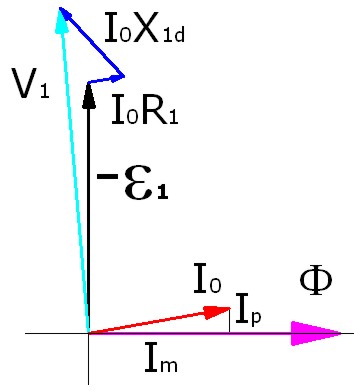
Esto supone que la tensión inducida en el primario ε1 ya no es igual a la de alimentación V1 , sino que hay que restar las caídas de tensión producidas por la resistencia de la bobina, así como la inductancia producida por las pérdidas de flujo.
Podemos representar estas pérdidas en un diagrama vectorial como el de la figura.
 |
|
Imagen 23: Representación vectorial de un transformador real en vacío
Elaboración propia |
Todo lo contado en este apartado ocurre realmente en un transformador, pero en la práctica todas estas consideraciones no se efectúan pues los valores de R1 y X1d, así como i0 son muy pequeños y las pérdidas por ellos generadas también lo son (entre el 0,01% y el 0,1%). Esto justifica que el diagrama vectorial utilizado en muchas ocasiones sea el de la imagen 21 y no el que acabamos de ver.
Llegado este punto, solo queda conectar una carga en el secundario para comprobar que sucede con el transformador real en carga.
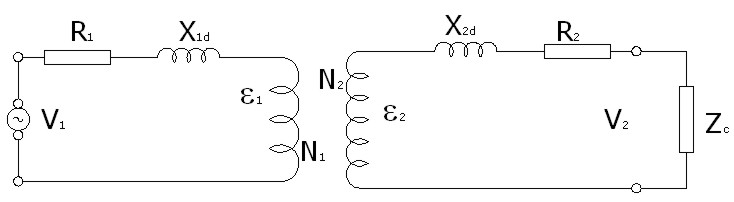
Los mismos efectos de pérdidas que en el primario sucederán en el secundario, es decir pérdidas de flujo, pérdidas resistivas en las bobinas y pérdidas en el núcleo, por lo que el esquema completo del transformador real será el que muestra la imagen.
 |
|
Imagen 24: Transformador real en carga
Elaboración propia |
Si ahora queremos conocer el valor de la tensión que podremos aplicar a la impedancia Zc a la salida del secundario, tendremos:
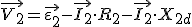 |
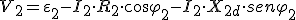 |
Al haber puesto una carga, circulará I2 por el secundario y eso, como ya se ha visto, provoca una corriente reflejada en el primario I'2 y teniendo en cuenta el nuevo valor de la corriente absorbida en vacío que se ha estudiado más arriba:
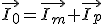 |
resultará que la corriente del primario en esta situación será:
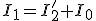 |
y teniendo en cuenta que I0 es muy pequeña frente a I'2 tendremos I1≈I'2 y la tensión inducida en el primario será:
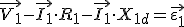 |
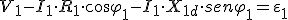 |
Se dispone de un transformador monofásico que tiene una relación de transformación de 80/1. La tensión del primario es de 20 KV y el transformador alimenta en el secundario a una carga de impedancia (1,64+j1,15)Ω. Si consideramos el transformador como ideal, se desea conocer:
- Tensión y corriente en el secundario.
- Corriente en el primario.
- Potencia activa y reactiva consumida por la carga.