Vamos a ver por último el concepto de impedancia, fíjate que en el circuito de la figura ya no aparece mención ninguna a que sea un circuito resistivo, inductivo o capacitivo. Veamos que es esa "Z" que aparece ahora en el circuito.

Imagen 13.
Fuente: Imagen prpia creada con Paint.

Por lo tanto vamos a definir una nueva magnitud que englobará a las anteriores y que denominaremos impedancia y representaremos por Z y se medirá en ohmios (Ω).

Aplicando la Ley de Ohm tenemos que:

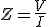
En un circuito de corriente alterna, el valor de Z seria equivalente al de R en un circuito de corriente continua. Por lo tanto podemos decir que la impedancia se opone al paso de corriente.

Has recordado en el tema anterior las operaciones con números complejos. La impedancia va a venir dada por un número complejo, en el que la parte real corresponderá con el valor de la resistencia y la parte imaginaria con la bobina o el condensador. A continuación lo puedes ver gráficamente.

Imagen 14. Circuito inductivo. Fuente: Elaboración propia creada con paint.	Imagen 15. Circuito capacitivo. Fuente: Elaboración propia creada con paint.