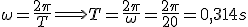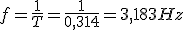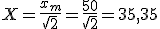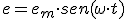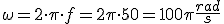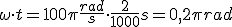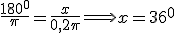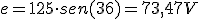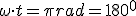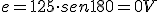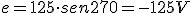1.1. Valores de una Onda Senoidal
En corriente alterna se suele trabajar con otros parámetros aparte de los ya mencionados, que en realidad son valores que toma la onda. Antes de que avances en este apartado, te tengo que decir que no debes asustarte por las integrales que aparecen, pues no se te pide que las resuelvas, aunque podrías hacerlo. Lo que realmente nos interesa son las expresiones finales que esas integrales nos dan y que son las que usaremos. Ahora sí, pasemos a ver algunos de ellos:
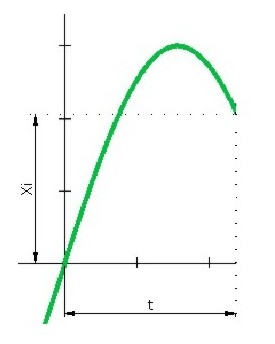
- Valor instantáneo: Es el que toma la ordenada (tensión o intensidad) en un instante, t, determinado.
 |
|
Imagen 4. Valor instantáneo. Fuente: Elaboración propia. |
- Valor de cresta o pico: Es el valor máximo que toma la onda y que conocemos como Amplitud.
- Valor medio Xm: antes de nada conviene aclarar que no es lo mismo Xm que xm. El primero, en mayúsculas corresponde al valor medio y el segundo, en minúsculas, al valor máximo de cresta de la onda. Pues bien, se define valor medio como la media aritmética de todos los valores instantáneos que adquiere la onda en un intervalo de tiempo. Si analizamos un período, el valor medio será cero, pues los valores de la semionda positiva quedarán anulados por los de la semionda negativa. No obstante en las ondas senoidales se considera un semiperíodo. Su expresión matemática es:
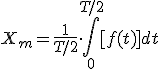 |
Recordando que la función senoidal f(t) era del tipo x=xmsen(ωt) y sustituyendo y resolviendo la integral, nos quedará:
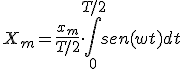
|
- Valor eficaz X: El valor eficaz de una corriente alterna es el valor que tendría una corriente continua que produjera la misma potencia que dicha corriente alterna, al aplicar ambas, primero una y luego otra, sobre una misma resistencia. Cuando decimos que la tensión de alimentación en un circuito es de 230 V nos estamos refiriendo a su valor eficaz. Al igual que en el caso anterior hay una expresión matemática para su obtención.
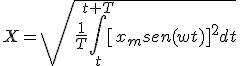 |
Si resolvemos la integral obtendremos la expresión que nos interesa:
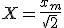 |
Vamos a aplicar las expresiones que acabamos de aprender con un ejercicio. Supongamos que tenemos una función senoidal del tipo x=50 sen(20t).
Deseamos conocer:
- El período y la frecuencia.
- La amplitud.
- Valor eficaz.
- Valor medio.
Tal vez te sea útil la siguiente animación. La finalidad de la misma no es complicarte la vida con el cálculo integral, sino hacerte ver que es posible con los conocimientos que tienes de matemáticas resolverla; de cualquier manera, lo que a ti se te pide es que sepas calcular el valor medio y eficaz de una corriente alterna.
|
|
|
Animación 1. Obtención del valor medio de una función senoidal.
Fuente: Elaboración propia. |