3. Método de mallas
El método de trabajo es muy similar al utilizado en el apartado anterior pero ahora vamos a asignar intensidades a cada una de las mallas en vez de rama por rama como hicimos anteriormente.
Consiste en aplicar la segunda ley de Kirchhoff a cada una de la R-(n-1) mallas independientes de la red, considerando como incógnitas las intensidades de cada una de las mallas, cuyo sentido determinaremos arbitrariamente con antelación.
R=ramas n=nudos
Una vez obtenidas las intensidades de cada malla será fácil obtener la intensidad de cada rama mediante la suma algebraica de las intensidades de las mallas a las que pertenece esa rama.
Las ramas exteriores tendrán una intensidad +/- la intensidad de la malla a la que pertenecen. El signo positivo o negativo dependerá de si coincide o no con la referencia de la intensidad de malla.
Cuando la rama pertenezca a dos mallas la intensidad vendrá como suma algebraica de las intensidades de dicha malla.
Veamos el ejercicio anterior pero ahora resuelto por mallas:
 |
|
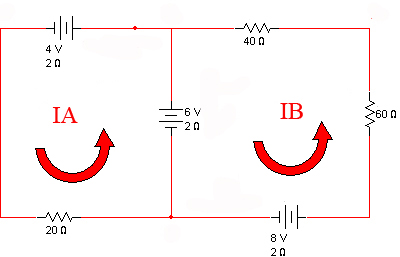
Imagen 10: Método de mallas - Circuito inicial |
Tenemos 3 ramas y 1 nudos, por tanto aplicaremos la segunda ley a Kirchhoff a 2 mallas independientes (3-(2-1))
Tomamos dos intensidades arbitrarias IA e IB, una para cada una de las mallas
Malla izquierda: 24*IA-2*IB=6-4
Malla derecha: 84*IB-2*IA=8-6
Resolviendo el sistema de dos ecuaciones con dos incógnitas:
IA=85*10-3 A (al ser positivo observamos que el sentido previsto por nosotros es correcto)
IB= 20,8*10-3 A (al ser positivo observamos que el sentido previsto por nosotros es correcto)
Nos faltaría obtener la intensidad que circula por la rama central que llamaremos IC. Para obtener este valor restaremos al valor de IA el valor de IB:
IC= 64,2*10-3 A (el sentido será el mismo que tiene IA)
Se puede observar que los resultados coinciden tanto si utilizamos Kirchhoff como si se utiliza el método de mallas.
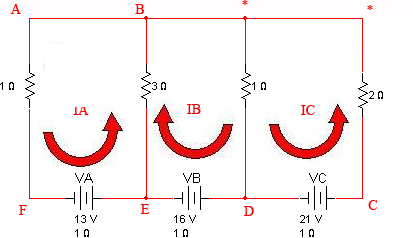
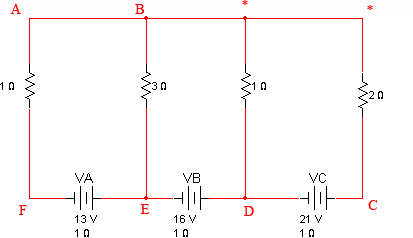
Utilizando el método de mallas obtener las intensidades que circulan por la red de la figura.
 |
|
Imagen 11. Imagen de elaboración propia |