3.1. Pirámides Regulares
Como la base de estas superficies debe ser un polígono regular (triángulo equilátero, cuadrado, pentágono, hexágono, etc..) la resolución de cualquier perspectiva isométrica debe pasar primero por la de dicha figura plana.
Así pues, siempre comenzaremos dibujando la perspectiva de la planta y luego determinaremos el vértice de la altura, todo ello aplicando el coeficiente de reducción isométrico.
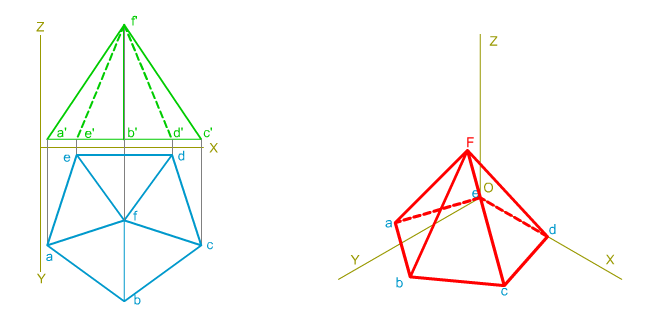
En la imagen superior te mostramos la perspectiva de una pirámide regular de base pentagonal, según sus vistas diédricas dadas.
Arista base paralela a un eje isométrico.
Como la base es un pentágono regular solamente puede tener una arista paralela a uno de los ejes de coordenadas isométricos.En este caso particular la arista está contenida en el eje X.
En la animación inferior te mostramos el procedimiento a seguir para trazar la perspectiva isométrica de dicha pirámide.
Aristas bases oblicuas a los ejes isométricos.
Dado que la base es un cuadrado todos las aristas bases están dispuestas oblicuamente respecto de los ejes de coordenadas isométricos.En este caso particular un vértice de la base está contenido en el centro O del triedro isométrico.
En la animación inferior puedes ver cómo se ha determinado la perspectiva de dicha pirámide.
|
|
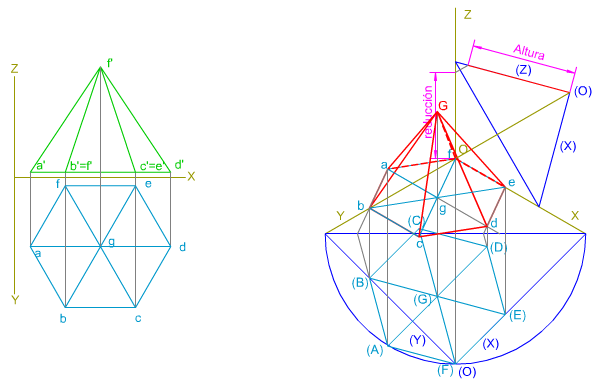
| En la imagen superior te mostramos cómo se ha trazado la perspectiva isométrica de una pirámide regular ABCDEFG de base hexagonal apoyada en el triedro XOY por su base ABCDEF.
Conocemos sus proyecciones diédricas, siendo dos aristas bases paralelas al eje isométrico X. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las herramientas de dibujo tradicionales. |