2.1. Intersección
Los fundamentos de la intersección, así como los dos métodos que podemos emplear, los hemos analizado en el apartado anterior.
Ahora vamos a desarrollarlos de manera más detallada, aplicándolo en los poliedros ya estudiados.
En el vídeo superior puedes recordar cómo se determina la intersección entre una recta y un plano.
Tetraedro, intersección con una recta horizontal.
Cuando una recta horizontal, o frontal, corta a un tetraedro determina de manera directa los puntos de intersección, ya que dicha recta estará contenida en un plano paralelo a uno de los de proyección.En este caso particular determinaremos la intersección entre una recta horizontal y un tetraedro conteniendo dicha recta en un plano horizontal auxiliar.
Hexaedro, intersección con una recta oblicua.
Como la recta oblicua corta a un hexaedro aplicaremos el segundo método estudiado en el primer apartado, así pues, contendremos la recta dada en un plano proyectante horizontal, determinando de manera directa los puntos intersección.
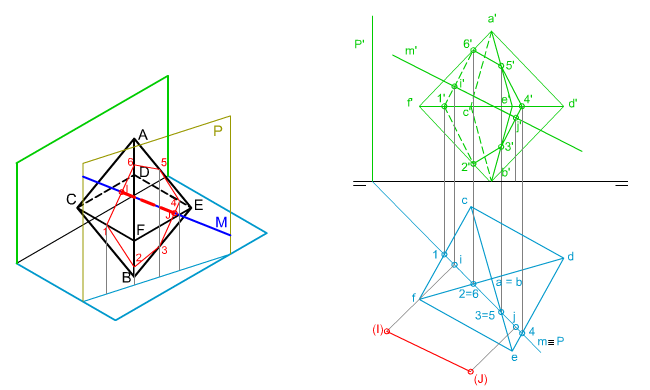
Octaedro, intersección con una recta oblicua.
En este último caso como la recta oblicua corta a un octaedro también aplicaremos el segundo método.
|
|
| En la imagen superior puedes ver cómo se ha determinado la verdadera magnitud del segmento intersección entre una recta dada M y un octaedro ABCDEF.
Conocemos las proyecciones diédricas de la recta y el poliedro. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para determinar la verdadera magnitud del segmento intersección IJ mediante las herramientas de dibujo tradicionales. |