2.2. Recta
RECTA.
Pueden darse dos casos:
- Que la recta sea cortada por el eje. El punto donde el eje de giro corta a la recta no se desplaza, basta entonces con coger otro punto de la recta.
- Que la recta y el eje se crucen .Como la recta queda definida por dos puntos sólo hay que girar dos de ellos, tomando uno de ellos como punto de tangencia de la circunferencia de giro.
Posiciones del eje de giro respecto de la recta.
- El eje y la recta se cortan.
La cota y el alejamiento del punto intersección entre la recta y el eje no cambian, por tanto, solamente debemos girar un punto arbitrario de la recta, según el eje de giro.
En la animación inferior puedes ver cómo se ha girado horizontalmente una recta oblicua R mediante un eje vertical E que la intersecciona en uno de sus puntos (A), transformándola en frontal, para realizar dicho giro el punto arbitrario elegido ha sido la traza horizontal, lo que nos facilita y simplifica el trazado.
- El eje y la recta se cruzan.
En este caso como el eje y la recta no se cortan debemos girar dos de sus puntos.
El arco de giro y la recta son tangentes, por tanto, el primer punto que gira es el punto de tangencia, el otro punto puede ser uno cualquiera de dicha recta.
En la animación inferior puedes ver cómo se ha girado verticalmente una recta oblicua R mediante un eje E (recta de punta) que se cruza con dicha recta, transformándola en otra recta oblicua cualquiera, para llevar a cabo el giro hemos trazado una recta perpendicular a la proyección vertical r' de la recta, obteniendo el punto de tangencia A (a'), siendo el segmento e'a' el radio de giro; observa cómo este método simplifica mucho el trazado, solamente nos queda seleccionar otro punto de la recta y girarlo según el ángulo de giro anterior.
GIRO HORIZONTAL.
Transformar una recta oblicua en frontal.
Dado que la recta es oblicua y se quiere transformar en frontal debemos variar su alejamiento, por tanto, el giro que tenemos que realizar debe ser horizontal.
Para simplificar el trazado se aconseja disponer el eje vertical de manera que corte a la recta y así solamente necesitemos girar un punto, mejor la traza horizontal.
Si necesitamos fijar un alejamiento concreto el eje vertical se dispondrá según este parámetro mediante una recta paralela a la LT.
En la siguiente animación te mostramos cómo gira horizontalmente una recta dada R según un eje vertical E, el ángulo de giro se ha tomado en sentido anti horario (positivo) de manera que la recta permanezca en el primer cuadrante.
GIRO VERTICAL.
Transformar una recta oblicua en horizontal.
En este caso queremos que la recta oblicua dada se transforme en una recta horizontal, por tanto, debemos cambiar su cota mediante un giro vertical.Como en el giro anterior se aconseja situar el eje de punta de manera que corte a la recta y así solamente necesitaremos girar un punto (la traza vertical).
Para determinar una cota concreta el eje de giro se dispondrá según este parámetro mediante una recta paralela a la LT.
En la animación inferior puedes ver cómo gira verticalmente una recta dada R según un eje de punta E, el ángulo de giro se ha tomado en sentido horario (negativo) de manera que la recta permanezca en el primer cuadrante.
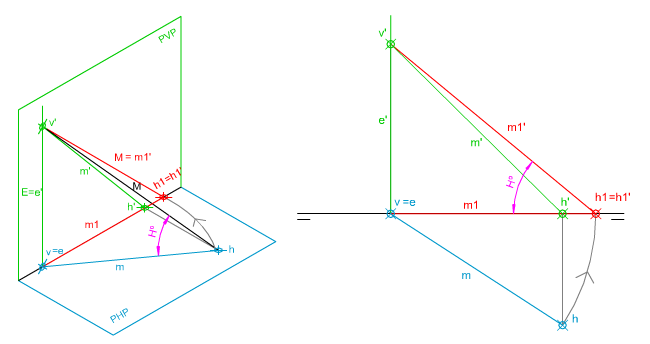 |
| En la imagen superior te mostramos cómo se ha girado una recta oblicua hasta situarla en el PVP.
Te pedimos que resuelvas dicho ejercicio mediante los utensilios de dibujo tradicionales. |