2.1. Punto
PUNTO.
Cuando un punto gira alrededor de un eje genera una circunferencia cuyo plano es perpendicular al eje tomado. El Centro de esta circunferencia es la traza del eje con el plano, siendo el radio la distancia del punto al eje.
Giro Horizontal.
Cuando giramos un punto horizontalmente este se desplaza sobre un plano horizontal, por tanto, su cota no varía; modificándose solamente el alejamiento.El ángulo de giro estará formado por los radios que unen el centro de giro con la proyección correspondiente.
En la animación inferior puedes ver cómo gira horizontalmente un punto dado A según un eje vertical E, el ángulo de giro se ha tomado en sentido horario (negativo) de manera que el alejamiento disminuya pero el punto permanezca en el primer cuadrante.
Giro Vertical.En este tipo de giro el punto se desplaza verticalmente sobre un plano frontal modificándose su cota pero no variando su alejamiento.
Como en el caso anterior, el ángulo de giro estará formado por los radios que unen el centro de giro con la proyección correspondiente.
En la siguiente animación te mostramos cómo gira verticalmente un punto dado A según un eje vertical E, el ángulo de giro se ha tomado en sentido anti horario (positivo) de manera que la cota disminuya pero el punto permanezca en el primer cuadrante.
Situar un punto conocido en una recta dada, determinando el eje de giro.Una de las aplicaciones más comunes en el giro de un punto es situarlo en un lugar determinado, en este caso vamos a contenerlo en una recta horizontal dada determinado la posición exacta del eje de giro.
Como la recta es horizontal el punto debe variar su cota, por tanto tenemos que realizar un giro vertical lo que nos indica que el eje de giro será una recta de punta.
En la animación inferior puedes ver cómo gira verticalmente un punto dado A hasta situarse sobre una recta horizontal M dada, como la cota del punto es mayor que la de la recta el eje de giro (recta de punta) estará situado por debajo de él.
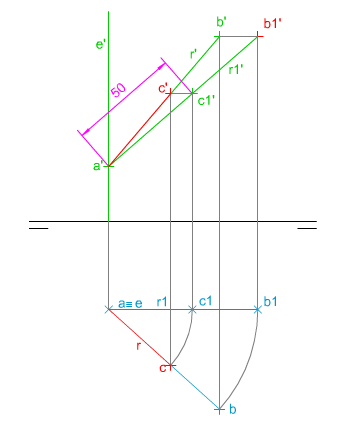 |
En la imagen izquierda te mostramos cómo se han determinado las proyecciones diédricas de un segmento distancia AC de 50 milímetros de longitud sobre una recta oblicua.
Para su trazado conocemos las proyecciones diédricas del punto extremo A y de la recta R. Te pedimos que, mediante las herramientas tradicionales de dibujo determines las proyecciones diédricas del segmento AC. |